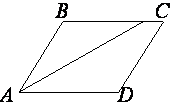Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 1°. Ответ дайте в градусах.
∠BCA=∠DAC=1° (т.к. это
накрест-лежащие углы)
А так как AC -
биссектриса, то ∠BAC=∠DAC=1°.
∠A=∠BAC+∠DAC=1°+1°=2°
Ответ: 2
Поделитесь решением
Присоединяйтесь к нам...
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=7.
Сторона ромба равна 60, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Радиус вписанной в квадрат окружности равен 22√2. Найдите диагональ этого квадрата.
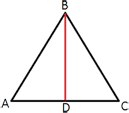Сторона равностороннего треугольника равна 10√
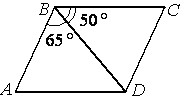Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: