В равнобедренную трапецию, периметр которой равен 200, а площадь равна 2000, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
SABCD=EF*(AD+BC)/2=2000
PABCD=AB+BC+CD+AD=200
AB=CD (так как
трапеция равнобедренная).
Чтобы окружность можно было вписать в трапецию должно выполняться условие - суммы противоположных сторон трапеции должны быть равны, т.е.
AD+BC=AB+CD
AD+BC=2AB (т.к. AB=CD)
Тогда:
PABCD=AB+BC+CD+AD=AB+2AB+AB=4AB=200
AB=50
Значит, AD+BC=2*50=100
SABCD=EF*(AD+BC)/2=EF*100/2=EF*50=2000
EF=40
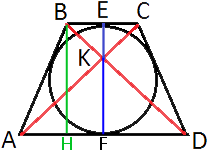Проведем
высоту BH, как показано на рисунке.
BH=EF=40, так как BEFH -
прямоугольник.
AH=(AD-BC)/2
По
теореме Пифагора:
AB2=BH2+AH2
502=402+AH2
2500=1600+AH2
900=AH2
30=AH=(AD-BC)/2
60=AD-BC, вспомним, что AD+BC=100
60=AD-(100-AD)
60=AD-100+AD
160=2AD
AD=80
Тогда BC=100-80=20
Рассмотрим треугольники AKF и CKE
AF=AD/2=40
CE=BC/2=10
∠AFK=∠CEK=90°
∠AKF=∠CKE (т.к. они
вертикальные)
По
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда, AF/CE=KF/KE
40/10=KF/KE
4=(EF-KE)/KE (вспомним, что EF=40)
4KE=40-KE
5KE=40
KE=8
Ответ: KE=8
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен
90°, то такой ромб — квадрат.
Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 170 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 340 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам.
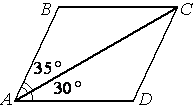Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
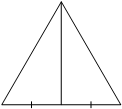Медиана равностороннего треугольника равна 13√3. Найдите его сторону.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: