
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ402 –ł–∑ 1087 |
 –ü—Ä—Ź–ľ–į—Ź, –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–į—Ź —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ AC —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC, –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł BC –≤ —ā–ĺ—á–ļ–į—Ö K –ł M —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ AC, –Ķ—Ā–Ľ–ł BK:KA=2:3, KM=14.
–ü—Ä—Ź–ľ–į—Ź, –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–į—Ź —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ AC —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC, –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł BC –≤ —ā–ĺ—á–ļ–į—Ö K –ł M —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ AC, –Ķ—Ā–Ľ–ł BK:KA=2:3, KM=14.
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł ABC –ł KBM.
/B - –ĺ–Ī—Č–ł–Ļ.
/BAC=/BKM (—ā.–ļ. —ć—ā–ĺ
—Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ —É–≥–Ľ—č)
/BCA=/BMK (—ā.–ļ. —ć—ā–ĺ —ā–ĺ–∂–Ķ
—Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ —É–≥–Ľ—č)
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, —ć—ā–ł —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł
–Ņ–ĺ–ī–ĺ–Ī–Ĺ—č –Ņ–ĺ
–Ņ–Ķ—Ä–≤–ĺ–ľ—É –Ņ—Ä–ł–∑–Ĺ–į–ļ—É –Ņ–ĺ–ī–ĺ–Ī–ł—Ź.
–Ę–ĺ–≥–ī–į –Ņ–ĺ
–ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é –Ņ–ĺ–ī–ĺ–Ī–Ĺ—č—Ö —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤:
BA/BK=AC/KM
(BK+KA)/BK=AC/KM
BK/BK+KA/BK=AC/KM
1+KA/BK=AC/KM
1+3/2=AC/14
2/2+3/2=AC/14
5/2=AC/14
5/2=AC/14
AC=5*14/2=35
–ě—ā–≤–Ķ—ā: AC=35
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
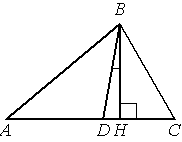 –í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ –ź–í–° —É–≥–Ľ—č –ź –ł –° —Ä–į–≤–Ĺ—č 40¬į –ł 60¬į —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ –ľ–Ķ–∂–ī—É –≤—č—Ā–ĺ—ā–ĺ–Ļ –í–Ě –ł –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–ĺ–Ļ BD.
–í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ –ź–í–° —É–≥–Ľ—č –ź –ł –° —Ä–į–≤–Ĺ—č 40¬į –ł 60¬į —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ –ľ–Ķ–∂–ī—É –≤—č—Ā–ĺ—ā–ĺ–Ļ –í–Ě –ł –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–ĺ–Ļ BD.
–ö–į–ļ–ł–Ķ –ł–∑ –ī–į–Ĺ–Ĺ—č—Ö —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ļ –≤–Ķ—Ä–Ĺ—č? –ó–į–Ņ–ł—ą–ł—ā–Ķ –ł—Ö –Ĺ–ĺ–ľ–Ķ—Ä–į.
1) –Ě–į –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ–į—Ź —ā–ĺ—á–ļ–į, —Ä–į–≤–Ĺ–ĺ—É–ī–į–Ľ—Ď–Ĺ–Ĺ–į—Ź –ĺ—ā –ļ–ĺ–Ĺ—Ü–ĺ–≤ –ĺ—ā—Ä–Ķ–∑–ļ–į.
2) –¶–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –≤ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ā–ĺ—á–ļ–į –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –Ķ–≥–ĺ –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā.
3) –ē—Ā–Ľ–ł –≥–ł–Ņ–ĺ—ā–Ķ–Ĺ—É–∑–į –ł –ĺ—Ā—ā—Ä—č–Ļ —É–≥–ĺ–Ľ –ĺ–ī–Ĺ–ĺ–≥–ĺ –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ —Ä–į–≤–Ĺ—č –≥–ł–Ņ–ĺ—ā–Ķ–Ĺ—É–∑–Ķ –ł —É–≥–Ľ—É –ī—Ä—É–≥–ĺ–≥–ĺ –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į, —ā–ĺ —ā–į–ļ–ł–Ķ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł —Ä–į–≤–Ĺ—č.
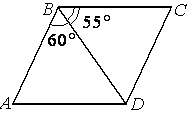 –Ē–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć BD –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į ABCD –ĺ–Ī—Ä–į–∑—É–Ķ—ā —Ā –Ķ–≥–ĺ —Ā—ā–ĺ—Ä–ĺ–Ĺ–į–ľ–ł —É–≥–Ľ—č, —Ä–į–≤–Ĺ—č–Ķ
60¬į –ł 55¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –ľ–Ķ–Ĺ—Ć—ą–ł–Ļ —É–≥–ĺ–Ľ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į.
–Ē–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć BD –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į ABCD –ĺ–Ī—Ä–į–∑—É–Ķ—ā —Ā –Ķ–≥–ĺ —Ā—ā–ĺ—Ä–ĺ–Ĺ–į–ľ–ł —É–≥–Ľ—č, —Ä–į–≤–Ĺ—č–Ķ
60¬į –ł 55¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –ľ–Ķ–Ĺ—Ć—ą–ł–Ļ —É–≥–ĺ–Ľ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į.
 –Ď–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā—č —É–≥–Ľ–ĺ–≤ A –ł B –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į ABCD –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –≤ —ā–ĺ—á–ļ–Ķ K. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į, –Ķ—Ā–Ľ–ł BC=5, –į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —ā–ĺ—á–ļ–ł K –ī–ĺ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB —Ä–į–≤–Ĺ–ĺ 5.
–Ď–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā—č —É–≥–Ľ–ĺ–≤ A –ł B –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į ABCD –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –≤ —ā–ĺ—á–ļ–Ķ K. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į, –Ķ—Ā–Ľ–ł BC=5, –į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —ā–ĺ—á–ļ–ł K –ī–ĺ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB —Ä–į–≤–Ĺ–ĺ 5.
 –í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC AB=BC=53, AC=56. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É –ľ–Ķ–ī–ł–į–Ĺ—č BM.
–í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC AB=BC=53, AC=56. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É –ľ–Ķ–ī–ł–į–Ĺ—č BM.

–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł:
(2015-03-03 20:38:43) –ē–Ľ–Ķ–Ĺ–į: –Ē–į, —Ā–Ņ–į—Ā–ł–Ī–ĺ –Ī–ĺ–Ľ—Ć—ą–ĺ–Ķ
(2015-03-03 17:28:35) –ź–ī–ľ–ł–Ĺ–ł—Ā—ā—Ä–į—ā–ĺ—Ä: –ē–Ľ–Ķ–Ĺ–į, —Ź –ī–ĺ–Ī–į–≤–ł–Ľ –≤ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ –Ņ–ĺ–ī—Ä–ĺ–Ī–Ĺ–ĺ—Ā—ā–Ķ–Ļ. –Ę–į–ļ –Ņ–ĺ–Ĺ—Ź—ā–Ĺ–ĺ?
(2015-03-03 15:55:25) –ē–Ľ–Ķ–Ĺ–į: –ü–ĺ–ī—Ā–ļ–į–∂–ł—ā–Ķ, –Ņ–ĺ–∂–į–Ľ—É–Ļ—Ā—ā–į, –≤ 4 —Ā—ā—Ä–ĺ–ļ–Ķ —Ā–Ĺ–ł–∑—É –ĺ—ā –ě—ā–≤–Ķ—ā–į, –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ –ī–ĺ–Ľ–∂–Ĺ–ĺ –Ī—č—ā—Ć "2+3" –≤ —á–ł—Ā–Ľ–ł—ā–Ķ–Ľ–Ķ?