
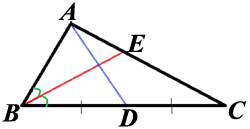 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны
и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны
и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.
Вариант №1
 Рассмотрим треугольник ABD.
Рассмотрим треугольник ABD.
BO перпендикулярен AD (по условию задачи), т.е. ∠BOD=∠BOA=90°.
∠ABO=∠DBO (т.к. BE -
биссектриса).
Получается, что треугольники ABO и DBO равны (по
второму признаку равенства треугольников).
Следовательно, AB=BD.
Т.е. треугольник ABD -
равнобедренный.
BO -
биссектриса этого треугольника, следовательно и
медиана, и
высота (по третьему
свойству равнобедренного треугольника).
Следовательно, AO=OD=AD/2=44/2=22.
 Проведем отрезок ED и рассмотрим треугольник BEC.
Проведем отрезок ED и рассмотрим треугольник BEC.
ED -
медиана этого треугольника, так как делит сторону BC пополам.
Площади треугольников EDC и EDB равны (по второму
свойству медианы).
SEDC=SEDB=(BE*OD)/2=(44*22)/2=22*22=484
SABE=(BE*AO)/2=(44*22)/2=484
Т.е. SABE=SEDC=SEDB=484
Тогда, SABС=3*484=1452
AD -
медиана треугольника ABC (по условию), следовательно делит треугольник на два равных по площади треугольника ABD и ACD (по
второму свойству медианы).
SABD=(AD*BO)/2=SABC/2
(44*BO)/2=1452/2
BO=1452/44=33
Рассмотрим треугольник ABO, он
прямоугольный, тогда применим
теорему Пифагора:
AB2=BO2+AO2
AB2=332+222
AB2=1089+484=1573
AB=√
BC=2AB=2*11√
Рассмотрим треугольник AOE.
OE=BE-BO=44-33=11
Так как этот треугольник тоже
прямоугольный, то можно применить
теорему Пифагора:
AE2=AO2+OE2
AE2=222+112=484+121=605
AE=√
Так как BE -
биссектриса, то используя ее
первое свойство запишем:
BC/AB=CE/AE
22√
2=CE/(11√
CE=22√
AC=AE+CE=11√
Ответ: AB=11√
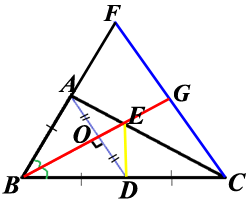 Проведём через точку C прямую, параллельную AD. Продлим BA и BE до пересечения с этой прямой в точках F и G соответственно.
Проведём через точку C прямую, параллельную AD. Продлим BA и BE до пересечения с этой прямой в точках F и G соответственно.Поделитесь решением
Присоединяйтесь к нам...
 Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и ADB подобны.
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и ADB подобны.
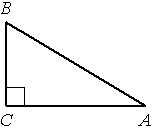 В треугольнике ABC угол C прямой, BC=3, cosB=0,6. Найдите AB.
В треугольнике ABC угол C прямой, BC=3, cosB=0,6. Найдите AB.
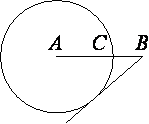 На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
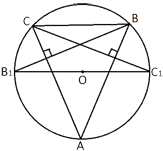 Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
 Найдите угол, который образуют минутная и часовая стрелки часов в 11:00. Ответ дайте в градусах.
Найдите угол, который образуют минутная и часовая стрелки часов в 11:00. Ответ дайте в градусах.



Комментарии: