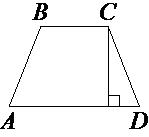Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.
Проведем отрезок из точки B перпендикулярно AD, как показано на рисунке.
BCEF - прямоугольник.
Рассмотрим треугольники ABF и DCE.
∠BAF=∠CDE (по второму свойству равнобедренной трапеции).
∠BFA=∠CED=90°
Следовательно, ∠ABF=∠DCE (по теореме о сумме углов треугольника).
AB=CD (по определению равнобедренной трапеции).
Тогда, по второму признаку данные треугольники равны.
Следовательно AF=DE=1.
FE=AE-DE=5-1=4
BC=FE=4 (по свойству прямоугольника).
Ответ: 4
Поделитесь решением
Присоединяйтесь к нам...
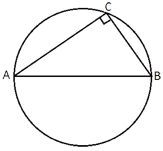В треугольнике ABC AC=15, BC=5√
естница соединяет точки A и B и состоит из 40 ступеней. Высота каждой ступени равна 19,5 см, а длина – 40 см. Найдите расстояние между точками A и B (в метрах).
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Один из острых углов прямоугольного треугольника равен 57°. Найдите его другой острый угол. Ответ дайте в градусах.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: