
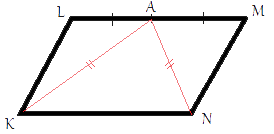
 В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA=NA. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA=NA. Докажите, что данный параллелограмм — прямоугольник.
Рассмотрим треугольники KLA и NMA. LA=MA, т.к. точка А - середина LM, AK=AN из условия задачи, LK=MN (по свойству параллелограмма). Соответственно, треугольники KLA и NMA равны (по третьему признаку равенства треугольников).
Из равенства этих треугольников следует, что ∠KLA=∠NMA.
LK||MN (по определению параллелограмма), рассмотрим сторону LM как секущую к этим параллельным сторонам. Тогда получается, что сумма углов KLA и NMA равна 180°, т.к. эти углы являются внутренними односторонними. Отсюда следует, что каждый из этих углов равен 90°.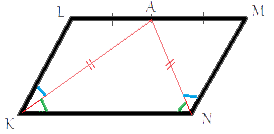 Рассмотрим треугольник KAN, KA=NA (по условию задачи), соответственно, этот треугольник
равнобедренный. Отсюда следует, что ∠AKN=∠ANK (
из свойства равнобедренного треугольника). Из ранее полученного равенства треугольников, следует, что ∠LKA=∠MNA. Получаем, что углы LKN и MNK равны.
Рассмотрим треугольник KAN, KA=NA (по условию задачи), соответственно, этот треугольник
равнобедренный. Отсюда следует, что ∠AKN=∠ANK (
из свойства равнобедренного треугольника). Из ранее полученного равенства треугольников, следует, что ∠LKA=∠MNA. Получаем, что углы LKN и MNK равны.
В свою очередь они так же являются внутренними односторонними и их сумма равна 180°. Получается, что и эти углы равны 90° каждый.
Параллелограмм, у которого все углы прямые (т.е. 90°) называется прямоугольником (по определению).
Поделитесь решением
Присоединяйтесь к нам...
 Радиус окружности, описанной около квадрата, равен 48√2. Найдите радиус окружности, вписанной в этот квадрат.
Радиус окружности, описанной около квадрата, равен 48√2. Найдите радиус окружности, вписанной в этот квадрат.
 Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол трапеции. Ответ дайте в градусах.
Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол трапеции. Ответ дайте в градусах.
Синус острого угла A треугольника ABC равен 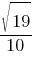 . Найдите CosA.
. Найдите CosA.
 Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АВ, если сторона АС равна 4.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АВ, если сторона АС равна 4.
 Проектор полностью освещает экран A высотой 50 см, расположенный на расстоянии 140 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 260 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Проектор полностью освещает экран A высотой 50 см, расположенный на расстоянии 140 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 260 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?



Комментарии: