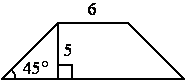В равнобедренной трапеции известны высота, меньшее основание и угол при основании. Найдите большее основание.
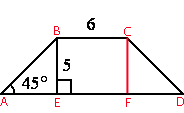Проведем
высоту CF.
Рассмотрим треугольники ABE и DCF.
∠BAE=∠CDF=45° (по
свойству равнобедренной трапеции).
∠BEA=∠CFD=90° (так как BE и CF -
высоты).
Используя
теорему о сумме углов треугольника, получаем, что:
∠EBA=∠FCD
AB=CD (по
определению равнобедренной трапеции).
Следовательно, данные треугольники равны (по
второму признаку равенства треугольников).
Значит, AE=FD.
Рассмотрим треугольник ABE.
По
определению tg∠BAE=BE/AE
tg45°=5/AE=1 (по
таблице)
AE=5
EF=BC=6 (так как BCFE -
прямоугольник)
AD=AE+EF+FD=5+6+5=16
Ответ: AD=16
Поделитесь решением
Присоединяйтесь к нам...
Основания равнобедренной трапеции равны 16 и 96, боковая сторона равна 58. Найдите длину диагонали трапеции.
Сторона AB параллелограмма ABCD вдвое больше стороны AD. Точка K — середина стороны AB. Докажите, что DK — биссектриса угла ADC.
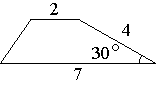Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 7.
Окружности радиусов 45 и 90 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 39 и 42, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: