
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 8 и 7. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 8 и 7. Найдите площадь параллелограмма ABCD.
 По
свойству касательной:
По
свойству касательной:
OF - радиус окружности, т.к. OF проходит через центр окружности и перпендикулярен
касательной AC.
AG=AF
BG=BH=x
CH=CF=y
AF найдем по
теореме Пифагора:
AO2=AF2+OF2
252=AF2+72
625=AF2+49
AF2=576
AF=24=AG
EH -
высота параллелограмма. EH=OH+OE=7+8=15
SABC=p*r, где p - полупериметр, r - радиус вписанной окружности.
p=(AB+BC+AC)/2.
Рассмотрим треугольники ABC и CDA.
AD=BC и AB=CD (по
свойству параллелограмма).
AC - общая сторона.
Следовательно, по
третьему признаку равенства треугольников, данные треугольники равны.
Тогда:
SABCD=2*SABC
И в тоже время SABCD=EH*AD.
Приравняем полученные равенства:
p*r=EH*AD/2
(AB+BC+AC)/2*r=EH*BC/2
(AG+GB+BH+HC+CF+AF)*r=EH*(BH+HC)
(24+x+x+y+y+24)*7=15*(x+y)
(48+2x+2y)*7=15*(x+y)
336+7(2x+2y)=15*(x+y)
336+14(x+y)=15*(x+y)
336=x+y
x+y=BC=AD
SABCD=EH*AD=15*336=5040
Ответ: SABCD=5040
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 6. Окружность радиуса 4,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
 Точка O – центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR – ромб. Найдите угол ORQ. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR – ромб. Найдите угол ORQ. Ответ дайте в градусах.
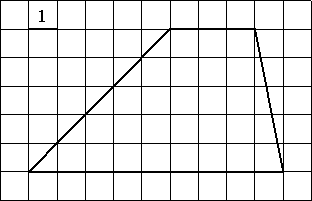 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
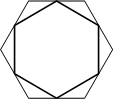 Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
 В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 30°. Найдите величину угла OAB.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 30°. Найдите величину угла OAB.



Комментарии:
(2017-03-31 09:02:01) Иван: спасибо за помощь в решении задачи
(2017-03-25 19:26:01) Администратор: Елена, все зависит от трапеции: обычная, прямая или равнобокая...
(2017-03-24 02:40:33) Елена: Подобная задача с трапецией как решается ?
(2017-03-01 16:40:49) Алевтина: Спасибо,красивое решение
(2015-02-14 11:07:15) Администратор: Лариса, очень рад, что Вы разобрались самостоятельно.
(2015-02-14 10:57:06) Лариса.: Ой поняла, это же расстояние от точки О до прямых.
(2015-02-13 22:10:27) Лариса.: Ой поняла, это же расстояние от точки О до прямых.
(2015-02-13 22:04:11) Лариса.: Спасибо Вам большое за ваш сайт. Вопрос по этой задаче. А почему ОF равен 7?
(2014-06-03 19:02:25) : спасибо!
(2014-05-27 15:06:25) Администратор: Алид, центр окружность обязательно лежит на EH. Смотрите, OE - расстояние от центра до AD, поэтому OE перпендикулярен AD. OH - радиус, проведенный к касательной BC, следовательно OH перпендикулярен BC. AD||BC, следовательно EH - прямая.
(2014-05-27 05:11:17) Алид: Узкое место: центр окружности O лежит на прямой EH. Мне это не кажется очевидным фактом. Если это не так, то решение некорректно. С уважением - Алид. Спасибо за решение