
 На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=2, BH=18. Найдите CH.
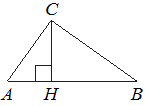
На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=2, BH=18. Найдите CH.
Рассмотрим треугольники ACH и BCH.
Докажем, что это подобные треугольники:
∠AHC=∠BHC=90° (так как CH -
высота).
По
теореме о сумме углов треугольника:
180°=∠CAH+∠AHC+∠HCA
180°=∠CAH+90°+∠HCA
90°=∠CAH+∠HCA
∠CAH=90°-∠HCA
Заметим, что:
∠BCH=90°-∠HCA
Получается, что ∠CAH=∠BCH
Тогда, по первому признаку подобия, данные треугольники подобны, т.е. можем записать пропорцию:
AH/CH=CH/BH
AH*BH=CH2
2*18=CH2
36=CH2
CH=√36=6
Ответ: 6
Поделитесь решением
Присоединяйтесь к нам...
 Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АВ, если сторона АС равна 4.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АВ, если сторона АС равна 4.
 В треугольнике ABC угол C прямой, AC=8, cosA=0,4. Найдите AB.
В треугольнике ABC угол C прямой, AC=8, cosA=0,4. Найдите AB.
 Сторона ромба равна 30, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 30, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
 Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 36.
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 36.
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=3 и MB=12. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=3 и MB=12. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.


Комментарии:
(2024-02-28 13:41:15) Юля: Прямая параллельная стороне АС треугольника АВС , пересекает стороны АВ и ВС в точках М и N соответственно. АВ =8 , АС =8 , МN= 2 Найдите АМ