
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ635 –Є–Ј 1087 |
 –Т —В—А–∞–њ–µ—Ж–Є–Є ABCD –±–Њ–Ї–Њ–≤–∞—П —Б—В–Њ—А–Њ–љ–∞ AB –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є—О BC. –Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —В–Њ—З–Ї–Є C –Є D –Є –Ї–∞—Б–∞–µ—В—Б—П –њ—А—П–Љ–Њ–є AB –≤ —В–Њ—З–Ї–µ E. –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є E –і–Њ –њ—А—П–Љ–Њ–є CD, –µ—Б–ї–Є AD=14, BC=12.
–Т —В—А–∞–њ–µ—Ж–Є–Є ABCD –±–Њ–Ї–Њ–≤–∞—П —Б—В–Њ—А–Њ–љ–∞ AB –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є—О BC. –Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —В–Њ—З–Ї–Є C –Є D –Є –Ї–∞—Б–∞–µ—В—Б—П –њ—А—П–Љ–Њ–є AB –≤ —В–Њ—З–Ї–µ E. –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є E –і–Њ –њ—А—П–Љ–Њ–є CD, –µ—Б–ї–Є AD=14, BC=12.
–Я–Њ —Г—Б–ї–Њ–≤–Є—О –Ј–∞–і–∞—З–Є AB –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–∞ BC, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–∞ –Є AD (—В.–Ї. –≤
—В—А–∞–њ–µ—Ж–Є–Є –Њ—Б–љ–Њ–≤–∞–љ–Є—П –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л).
–†–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –Х –і–Њ –њ—А—П–Љ–Њ–є CD - –Њ—В—А–µ–Ј–Њ–Ї, –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Л–є CD –Є –њ—А–Њ—Е–Њ–і—П—Й–Є–є —З–µ—А–µ–Ј —В–Њ—З–Ї—Г –Х.
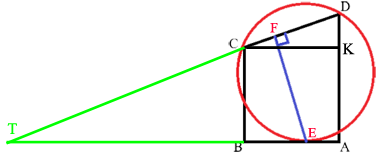 –Я—А–Њ–і–Њ–ї–ґ–Є–Љ —Б—В–Њ—А–Њ–љ—Л AB –Є CD –і–Њ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –≤ —В–Њ—З–Ї–µ T.
–Я—А–Њ–і–Њ–ї–ґ–Є–Љ —Б—В–Њ—А–Њ–љ—Л AB –Є CD –і–Њ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –≤ —В–Њ—З–Ї–µ T.
–Я—А–Њ–≤–µ–і–µ–Љ CK –њ–∞—А–∞–ї–ї–µ–ї—М–љ–Њ AB.
AK=B–° (—В.–Ї. ABKC -
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї).
KD=AD-AK=14-12=2
–Я–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О –Ї–Њ—Б–Є–љ—Г—Б–∞: cos∠CDK=KD/CD=2/CD
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є TCB –Є CKD.
∠CTB=∠DCK (—В.–Ї. —Н—В–Њ
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ—Л–µ —Г–≥–ї—Л –њ—А–Є –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л—Е –њ—А—П–Љ—Л—Е TA –Є CK)
∠TBC=∠CKD=90¬∞
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, —Н—В–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є
–њ–Њ–і–Њ–±–љ—Л (–њ–Њ
–њ–µ—А–≤–Њ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г –њ–Њ–і–Њ–±–Є—П).
–Ґ–Њ–≥–і–∞, BC/KD=TC/CD
12/2=TC/CD
TC=6CD
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Њ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ –Є —Б–µ–Ї—Г—Й–µ–є:
TE2=TD*TC=(TC+CD)*TC=(6CD+CD)6CD=7CD*6CD=42CD2
TE=CD√
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є TEF –Є TAD.
∠CTB - –Њ–±—Й–Є–є
∠EFT=∠TAD=90¬∞
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –њ—А–Є–Љ–µ–љ–Є–≤
—В–µ–Њ—А–µ–Љ—Г –Њ —Б—Г–Љ–Љ–µ —Г–≥–ї–Њ–≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –њ–Њ–ї—Г—З–∞–µ–Љ, —З—В–Њ ∠TEF=∠ADT (=∠CDK).
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, cos∠TEF=cos∠ADT(=cos∠CDK).
EF=TE*cos∠TEF=TE*cos∠ADT=2TE/CD=2CD√
–Ю—В–≤–µ—В: EF=2√
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C —А–∞–≤–µ–љ 90¬∞, sinB=3/7, AB=21. –Э–∞–є–і–Є—В–µ AC.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C —А–∞–≤–µ–љ 90¬∞, sinB=3/7, AB=21. –Э–∞–є–і–Є—В–µ AC.
 –°—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 36, –∞ –Њ—Б—В—А—Л–є —Г–≥–Њ–ї —А–∞–≤–µ–љ 60¬∞. –Т—Л—Б–Њ—В–∞ —А–Њ–Љ–±–∞, –Њ–њ—Г—Й–µ–љ–љ–∞—П –Є–Ј –≤–µ—А—И–Є–љ—Л —В—Г–њ–Њ–≥–Њ —Г–≥–ї–∞, –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г –љ–∞ –і–≤–∞ –Њ—В—А–µ–Ј–Ї–∞. –Ъ–∞–Ї–Њ–≤—Л –і–ї–Є–љ—Л —Н—В–Є—Е –Њ—В—А–µ–Ј–Ї–Њ–≤?
–°—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 36, –∞ –Њ—Б—В—А—Л–є —Г–≥–Њ–ї —А–∞–≤–µ–љ 60¬∞. –Т—Л—Б–Њ—В–∞ —А–Њ–Љ–±–∞, –Њ–њ—Г—Й–µ–љ–љ–∞—П –Є–Ј –≤–µ—А—И–Є–љ—Л —В—Г–њ–Њ–≥–Њ —Г–≥–ї–∞, –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г –љ–∞ –і–≤–∞ –Њ—В—А–µ–Ј–Ї–∞. –Ъ–∞–Ї–Њ–≤—Л –і–ї–Є–љ—Л —Н—В–Є—Е –Њ—В—А–µ–Ј–Ї–Њ–≤?
 –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–≥–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–≥–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
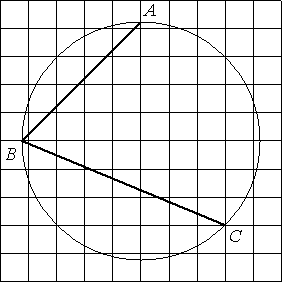 –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABC. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABC. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –¶–µ–љ—В—А–∞–ї—М–љ—Л–є —Г–≥–Њ–ї AOB –Њ–њ–Є—А–∞–µ—В—Б—П –љ–∞ —Е–Њ—А–і—Г –Р–Т —В–∞–Ї, —З—В–Њ —Г–≥–Њ–ї –Ю–Р–Т —А–∞–≤–µ–љ 60¬∞. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —Е–Њ—А–і—Л –Р–Т, –µ—Б–ї–Є —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ 7.
–¶–µ–љ—В—А–∞–ї—М–љ—Л–є —Г–≥–Њ–ї AOB –Њ–њ–Є—А–∞–µ—В—Б—П –љ–∞ —Е–Њ—А–і—Г –Р–Т —В–∞–Ї, —З—В–Њ —Г–≥–Њ–ї –Ю–Р–Т —А–∞–≤–µ–љ 60¬∞. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —Е–Њ—А–і—Л –Р–Т, –µ—Б–ї–Є —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ 7.


–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2017-06-03 19:47:21) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ъ–∞—В—П, —П –њ–Њ–і–њ–Є—Б–∞–ї –≤ —А–µ—И–µ–љ–Є–Є, —З—В–Њ–±—Л —Б—В–∞–ї–Њ –њ–Њ–љ—П—В–љ–µ–є. ∠ADT - —Н—В–Њ ∠CDK, –Ї–Њ—В–Њ—А—Л–є —А–∞–≤–µ–љ 2/CD (—Н—В–Њ –Љ—Л –љ–∞—И–ї–Є —А–∞–љ–µ–µ).
(2017-06-03 01:35:19) –Ъ–∞—В—П: –Ю–±—К—П—Б–љ–Є—В–µ –њ–Њ–ґ–∞–ї—Г–є—Б—В–∞ –њ–Њ—Б–ї–µ–і–љ—О—О —Б—В—А–Њ—З–Ї—Г –≤ —А–µ—И–µ–љ–Є–Є : –њ–Њ—З–µ–Љ—Г –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –Ї–Њ—Б–Є–љ—Г—Б–∞ —Г–≥–ї–∞ ADT –љ–∞ TE —А–∞–≤–љ–Њ 2TE/CD?