В треугольнике ABC с тупым углом ABC проведены высоты AA1 и CC1. Докажите, что треугольники A1BC1 и ABC подобны.
Рассмотрим треугольники AA1B и CC1B.
∠ABA1=∠CBC1, так как они
вертикальные.
∠AA1B=∠CC1B, так как они прямые по условию задачи.
Следовательно, по
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда, по
определению подобных треугольников:
AB/BC=A1B/C1B
Преобразуем это равенство:
AB/A1B=BC/C1B
Рассмотрим треугольники A1BC1 и ABC.
∠ABC=∠A1BC1, так как они
вертикальные.
Тогда, по
второму признаку подобия, данные треугольники
подобны.
Поделитесь решением
Присоединяйтесь к нам...
Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
Катеты прямоугольного треугольника равны 3√
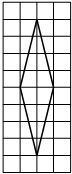На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите площадь этого ромба.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=15, MD=3, H — точка пересечения высот треугольника ABC. Найдите AH.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-11-27 18:14:34) Любовь: Спасибо за помощь и за создание такого прекрасного сайта.