Основания BC и AD трапеции ABCD равны соответственно 4 и 64, BD=16. Докажите, что треугольники CBD и ADB подобны.
ABCD -
трапеция, следовательно, AD||BC.
∠CBD=∠ADB (т.к. это
накрест-лежащие углы для параллельных прямых AD и BC).
Рассмотрим отношения сторон:
BC/BD=4/16=1/4
BD/AD=16/64=1/4
Тогда по
второму признаку подобия треугольников, треугольники CBD и ADB подобны.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC проведена биссектриса AL, угол ALC равен 152°, угол ABC равен 137°. Найдите угол ACB. Ответ дайте в градусах.
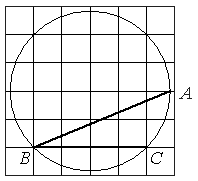Найдите угол ABC. Ответ дайте в градусах.
В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 6.
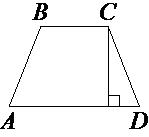Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.
В треугольнике ABC известно, что ∠BAC=64°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2019-03-22 19:41:52) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2019-03-21 11:46:08) : основание bc и ad трапеции abcd равны соответственно 2 и 32 BD=8 ДОКАЖИТЕ ЧТО ТРЕУГОЛЬНИКИ СBD и BDA подобны
(2016-02-24 20:57:13) Никита: Сайт просто супер, очень помогает !!!