
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ940 –ł–∑ 1087 |
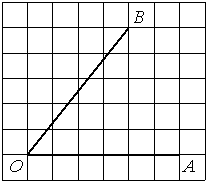 –Ě–į–Ļ–ī–ł—ā–Ķ —ā–į–Ĺ–≥–Ķ–Ĺ—Ā —É–≥–Ľ–į AOB, –ł–∑–ĺ–Ī—Ä–į–∂—Ď–Ĺ–Ĺ–ĺ–≥–ĺ
–Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ.
–Ě–į–Ļ–ī–ł—ā–Ķ —ā–į–Ĺ–≥–Ķ–Ĺ—Ā —É–≥–Ľ–į AOB, –ł–∑–ĺ–Ī—Ä–į–∂—Ď–Ĺ–Ĺ–ĺ–≥–ĺ
–Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ.
–ü—Ä–ĺ–≤–Ķ–ī–Ķ–ľ –≤—č—Ā–ĺ—ā—É –ł–∑ —ā–ĺ—á–ļ–ł –í –ļ –ĺ—ā—Ä–Ķ–∑–ļ—É OA, —á—ā–ĺ–Ī—č –Ņ–ĺ–Ľ—É—á–ł–Ľ—Ā—Ź
–Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ļ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ:
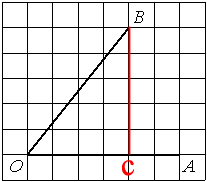 –ü–ĺ–Ľ—É—á–ł–Ľ—Ā—Ź —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ OBC —Ā –ļ–į—ā–Ķ—ā–į–ľ–ł –ě–° (–ī–Ľ–ł–Ĺ–į 4) –ł BC (–ī–Ľ–ł–Ĺ–į 5).
–ü–ĺ–Ľ—É—á–ł–Ľ—Ā—Ź —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ OBC —Ā –ļ–į—ā–Ķ—ā–į–ľ–ł –ě–° (–ī–Ľ–ł–Ĺ–į 4) –ł BC (–ī–Ľ–ł–Ĺ–į 5).
–ü–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é —ā–į–Ĺ–≥–Ķ–Ĺ—Ā–į:
tgAOB=BC/OC=5/4=1,25
–ě—ā–≤–Ķ—ā: 1,25
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
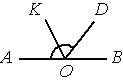 –Ě–į–Ļ–ī–ł—ā–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—É —É–≥–Ľ–į DOK, –Ķ—Ā–Ľ–ł OK ‚ÄĒ –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į —É–≥–Ľ–į AOD, ∠DOB=64¬į. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–Ě–į–Ļ–ī–ł—ā–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—É —É–≥–Ľ–į DOK, –Ķ—Ā–Ľ–ł OK ‚ÄĒ –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į —É–≥–Ľ–į AOD, ∠DOB=64¬į. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
 –ü–Ľ–ĺ—Č–į–ī—Ć –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–į 18√
–ü–Ľ–ĺ—Č–į–ī—Ć –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–į 18√
 –Ę–ĺ—á–ļ–ł M –ł N —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–į–ľ–ł —Ā—ā–ĺ—Ä–ĺ–Ĺ AB –ł BC —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –ě—ā—Ä–Ķ–∑–ļ–ł AN
–ł CM –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –≤ —ā–ĺ—á–ļ–Ķ O, AN=24, CM=15. –Ě–į–Ļ–ī–ł—ā–Ķ AO.
–Ę–ĺ—á–ļ–ł M –ł N —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–į–ľ–ł —Ā—ā–ĺ—Ä–ĺ–Ĺ AB –ł BC —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –ě—ā—Ä–Ķ–∑–ļ–ł AN
–ł CM –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –≤ —ā–ĺ—á–ļ–Ķ O, AN=24, CM=15. –Ě–į–Ļ–ī–ł—ā–Ķ AO.
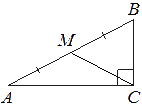 –í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC —É–≥–ĺ–Ľ C —Ä–į–≤–Ķ–Ĺ 90¬į, M ‚ÄĒ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB, AB=20, BC=10. –Ě–į–Ļ–ī–ł—ā–Ķ CM.
–í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC —É–≥–ĺ–Ľ C —Ä–į–≤–Ķ–Ĺ 90¬į, M ‚ÄĒ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB, AB=20, BC=10. –Ě–į–Ļ–ī–ł—ā–Ķ CM.
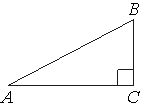 –í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC —É–≥–ĺ–Ľ C —Ä–į–≤–Ķ–Ĺ 90¬į, AC=4, AB=5. –Ě–į–Ļ–ī–ł—ā–Ķ sinB.
–í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC —É–≥–ĺ–Ľ C —Ä–į–≤–Ķ–Ĺ 90¬į, AC=4, AB=5. –Ě–į–Ļ–ī–ł—ā–Ķ sinB.

–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł: