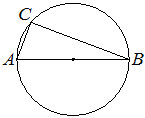
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если
угол BAC равен 74°. Ответ дайте в градусах.
По
теореме об описанной окружности, центр описанной окружности лежит на точке пересечения
серединных перпендикуляров сторон треугольника.
У
прямоугольного треугольника центр окрудности лежит на середине гипотенузы, так же как и в треугольнике нашей задачи, следовательно, данный треугольник
прямоугольный.
Следовательно, угол ACB=90°.
По
теореме о сумме углов треугольника:
180°=∠ACB+∠CBA+∠BAC
180°=90°+∠CBA+74°
∠CBA=180°-90°-74°
∠CBA=16°
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
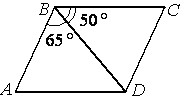Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
65° и 50°. Найдите меньший угол параллелограмма.
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и BDA подобны.
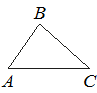В треугольнике ABC известно, что AB=5, BC=7, AC=9. Найдите cos∠ABC.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 9 м. Найдите длину троса.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2018-03-10 15:07:06) ПЕТЯ: центр окружности описанной около треугольника abc лежит на стороне ab НАЙДИТЕ УГОЛ АБС ЕСЛИ УГОЛ ВАС =33 РЕШУ
(2017-05-14 18:53:14) Администратор: Да, можно и так это определить.
(2017-05-13 18:44:14) : То, что треугольник прямоугольный следует из теоремы: вписанный угол, опирающийся на диаметр, равен 90 градусам