Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
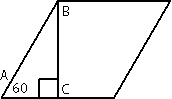Рассмотрим треугольник АВС.
Этот треугольник
прямоугольный (по условию задачи).
∠A=60°, следовательно по
теореме о сумме углов треугольника:
∠АВС = 180°-90°-60°=30°.
По второму свойству прямоугольного треугольника:
АС=АВ/2=32/2=16.
Следовательно вторая половина стороны ромба = 32-16=16.
Т.е., в данной задаче, высота, проведенная к стороне ромба делит эту сторону на две равные части.
Ответ: 16 и 16.
Поделитесь решением
Присоединяйтесь к нам...
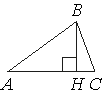В остроугольном треугольнике ABC проведена высота BH, ∠BAC=37°. Найдите угол ABH. Ответ дайте в градусах.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 17, а одна из диагоналей ромба равна 68. Найдите углы ромба.
Человек ростом 1,8 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 7,2 м. Найдите длину тени человека в метрах.
Радиус вписанной в квадрат окружности равен 7√
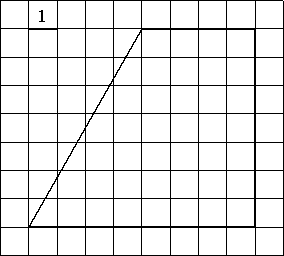Найдите площадь трапеции, изображённой на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: