Катеты прямоугольного треугольника равны 20 и 15. Найдите синус наименьшего угла этого треугольника.
Так как треугольник
прямоугольный, то можем применить
теорему Пифагора:
AB2=BC2+AC2
AB2=152+202
AB2=225+400=625
AB=25
Меньший угол лежит напротив меньшей стороны, 15<20, следовательно
синус меньшего угла будет равен
отношению меньшей стороны к гипотенузе, т.е. 15/25=3/5=0,6
Ответ: 0,6
Поделитесь решением
Присоединяйтесь к нам...
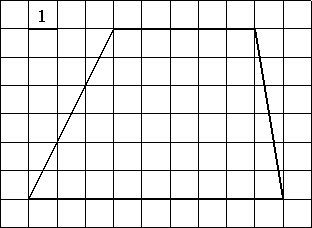Найдите площадь трапеции, изображённой на рисунке.
В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=54. Найдите площадь ромба.
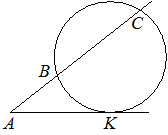Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=8, BC=24. Найдите AK.
Площадь равнобедренного треугольника равна 144√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-12-28 02:13:35) Администратор: Влад, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2016-12-25 22:08:36) влад: в прямоугольном треугольнике катеты раны 15 и 20 см. найти площадь