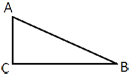
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 36 и 39.
Площадь
прямоугольного треугольника равна половине произведения катетов.
BC - катет длиной 36.
По
теореме Пифагора найдем второй катет:
AB2=AC2+BC2
392=AC2+362
1521=AC2+1296
225=AC2
AC=15
S=AC*BC/2=15*36/2=15*18=270
Ответ: S=270
Поделитесь решением
Присоединяйтесь к нам...
В трапеции ABCD AB=CD, ∠BDA=54° и ∠BDC=33°. Найдите угол ABD. Ответ дайте в градусах.
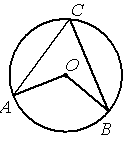Точка О – центр окружности, /AOB=110° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол STV. Ответ дайте в градусах.
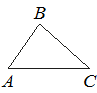В треугольнике ABC известно, что AB=5, BC=7, AC=9. Найдите cos∠ABC.
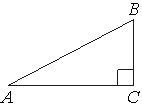В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-01-09 21:30:31) Администратор: Гоша, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2017-01-06 19:02:48) Гоша: Найдите площадь прямоугольного треугольника,если его катет и гипотенуза равны соответственно 18 и 30