ОГЭ, Математика. Геометрия: Задача №2921C7 | Ответ-Готов

Юмор

Автор: Таська
Так выглядит современная программа обучения.
�...читать далее

ОГЭ, Математика.
Геометрия: Задача №2921C7

Задача №513 из 1087
Условие задачи:

Площадь прямоугольного треугольника равна 2450√3/3. Один из острых углов равен 30°. Найдите длину катета, прилежащего к этому углу.

Решение задачи:

Площадь прямоугольного треугольника равна половине произведения катетов:
S=AC*BC/2=2450√3/3
Пусть 30-и градусам равен угол BAC.
Тангенс BAC:
td∠BAC=tg30°=BC/AC=√3/3 (по таблице).
BC=AC√3/3
S=AC*BC/2=2450√3/3
AC*BC=4900√3/3
AC*AC√3/3=4900√3/3
AC²=4900
AC=70
Ответ: 70

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №6AC1BC

Точка О – центр окружности, /ACB=24° (см. рисунок). Найдите величину угла AOB (в градусах).

Задача №1BA510

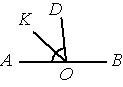Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=108°. Ответ дайте в градусах.

Задача №F63DA7

На стороне AC треугольника ABC отмечена точка D так, что AD=5, DC=7. Площадь треугольника ABC равна 60. Найдите площадь треугольника ABD.

Задача №09817E

Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол STV. Ответ дайте в градусах.

Задача №656C84

Площадь прямоугольного треугольника равна 968√3/3. Один из острых углов равен 60°. Найдите длину катета, лежащего напротив этого угла.

Комментарии:

Найти задачу

Подписаться на новости сайта

Хочу получать новые решения

email рассылки Ни какого спама

email рассылки

X Прямоугольный треугольник — это треугольник, в котором один угол прямой (то есть составляет 90°).
Сторона, противоположная прямому углу, называется гипотенузой (сторона c на рисунке).
Стороны, прилегающие к прямому углу, называются катетами.

X

Copyright otvet-gotov.ru 2014-2021. Все права защищены.