
 Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85.
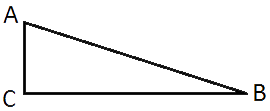
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85.
AB=85, AC=40
По
теореме Пифагора найдем второй катет:
AB2=AC2+BC2
852=402+BC2
BC2=7225-1600
BC2=5625
BC=75
Площадь любого треугольника равна половине произведения
высоты и стороны, к которой проведена
высота. В
прямоугольном треугольнике
высота совпадает с одним из катетов, получается, что площадь
прямоугольного треугольника равна половине произведения катетов.
SABC=(AC*BC)/2=(40*75)/2=1500
Ответ: 1500
Поделитесь решением
Присоединяйтесь к нам...
 Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
 Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.
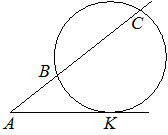 Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=2, AC=8. Найдите AK.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=2, AC=8. Найдите AK.
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.

Комментарии:
(2020-12-22 17:10:53) арсен: Найти неизвестный катет прямоугольного треугольника, если его гипотенуза равна 85 см, а один из катетов 13 см.