
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ405 –Є–Ј 1087 |
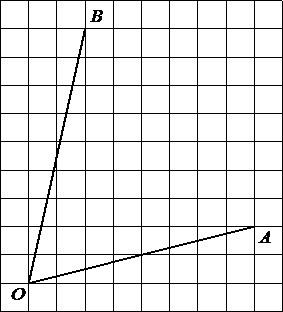 –Э–∞–є–і–Є—В–µ —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞
AOB.
–Э–∞–є–і–Є—В–µ —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞
AOB.
–Т–∞—А–Є–∞–љ—В вДЦ1 (–Я—А–Є—Б–ї–∞–ї –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї—М –Х–≤–≥–µ–љ–Є–є)
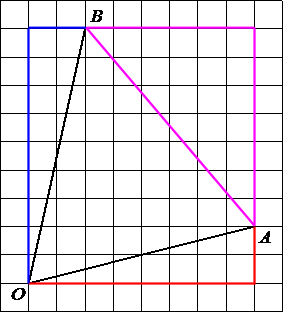 –Я—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Њ–Ї AB.
–Я—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Њ–Ї AB.
–Э–∞–є–і–µ–Љ –Ї–∞–ґ–і—Г—О —Б—В–Њ—А–Њ–љ—Г —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABO –њ–Њ
—В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞:
AO2=22+82
AO2=4+64=68
AO=√
AB2=72+62
AB2=49+36=85
AB=√
BO2=92+22
BO2=81+4=85
BO=√
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Ї–Њ—Б–Є–љ—Г—Б–Њ–≤:
AB2=AO2+BO2-2AO*BO*cos∠AOB
(√
85=4*17+85-4√
85=153-4√
-68=-4√
17=√
cos∠AOB=17/√
–Я–Њ –Њ—Б–љ–Њ–≤–љ–Њ–є —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–є —Д–Њ—А–Љ—Г–ї–µ:
sin2∠AOB+cos2∠AOB=1
sin2∠AOB+(17/√
sin2∠AOB+289/1445=1
sin2∠AOB+17/85=1
sin2∠AOB+1/5=1
sin2∠AOB=4/5
sin∠AOB=2/√
tg∠AOB=sin∠AOB/cos∠AOB=(2/√
–Ю—В–≤–µ—В: tg∠AOB=2
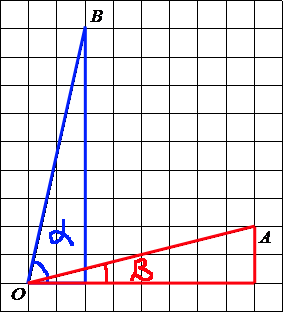 –Ф–Њ—Б—В—А–Њ–Є–Љ —З–µ—А—В–µ–ґ –і–Њ –і–≤—Г—Е
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤. –Э–∞–є–і–µ–Љ
—В–∞–љ–≥–µ–љ—Б—Л –і–ї—П –Њ–±–Њ–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ –і–ї—П –Є—Е —Г–≥–ї–Њ–≤ –Ю.
–Ф–Њ—Б—В—А–Њ–Є–Љ —З–µ—А—В–µ–ґ –і–Њ –і–≤—Г—Е
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤. –Э–∞–є–і–µ–Љ
—В–∞–љ–≥–µ–љ—Б—Л –і–ї—П –Њ–±–Њ–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ –і–ї—П –Є—Е —Г–≥–ї–Њ–≤ –Ю.–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Б —В—Г–њ—Л–Љ —Г–≥–ї–Њ–Љ ABC –њ—А–Њ–≤–µ–і–µ–љ—Л –≤—Л—Б–Њ—В—Л AA1 –Є CC1. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є A1BC1 –Є ABC –њ–Њ–і–Њ–±–љ—Л.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Б —В—Г–њ—Л–Љ —Г–≥–ї–Њ–Љ ABC –њ—А–Њ–≤–µ–і–µ–љ—Л –≤—Л—Б–Њ—В—Л AA1 –Є CC1. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є A1BC1 –Є ABC –њ–Њ–і–Њ–±–љ—Л.
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC AB=BC, –∞ –≤—Л—Б–Њ—В–∞ AH –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г BC –љ–∞ –Њ—В—А–µ–Ј–Ї–Є BH=52 –Є CH=13. –Э–∞–є–і–Є—В–µ cosB.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC AB=BC, –∞ –≤—Л—Б–Њ—В–∞ AH –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г BC –љ–∞ –Њ—В—А–µ–Ј–Ї–Є BH=52 –Є CH=13. –Э–∞–є–і–Є—В–µ cosB.
–Э–∞ –Ї–∞–Ї–Њ–є —Г–≥–Њ–ї (–≤ –≥—А–∞–і—Г—Б–∞—Е) –њ–Њ–≤–Њ—А–∞—З–Є–≤–∞–µ—В—Б—П –Љ–Є–љ—Г—В–љ–∞—П —Б—В—А–µ–ї–Ї–∞, –њ–Њ–Ї–∞ —З–∞—Б–Њ–≤–∞—П –њ–Њ–≤–Њ—А–∞—З–Є–≤–∞–µ—В—Б—П –љ–∞ 14¬∞?
 –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–µ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —А–∞–≤–µ–љ 10√3. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —Б—В–Њ—А–Њ–љ—Л —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–µ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —А–∞–≤–µ–љ 10√3. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —Б—В–Њ—А–Њ–љ—Л —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
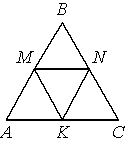 –Т —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–µ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —В–Њ—З–Ї–Є M, N, K вАФ —Б–µ—А–µ–і–Є–љ—Л —Б—В–Њ—А–Њ–љ –Р–Т, –Т–°, –°–Р —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –РMNK вАФ —А–Њ–Љ–±.
–Т —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–µ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —В–Њ—З–Ї–Є M, N, K вАФ —Б–µ—А–µ–і–Є–љ—Л —Б—В–Њ—А–Њ–љ –Р–Т, –Т–°, –°–Р —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –РMNK вАФ —А–Њ–Љ–±.

–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2015-05-16 19:18:34) –°–≤–µ—В–ї–∞–љ–∞: –Я–Њ–ї–љ–Њ—Б—В—М—О —Б–Њ–≥–ї–∞—Б–љ–∞ —Б –Х–ї–µ–љ–Њ–є. –Ф–ї—П —Г—З–∞—Й–Є—Е—Б—П 9 –Ї–ї–∞—Б—Б–∞ –µ—С —Б–њ–Њ—Б–Њ–± –≤ –≠–Ґ–Ю–Щ –Ј–∞–і–∞—З–µ —А–∞—Ж–Є–Њ–љ–∞–ї—М–љ–µ–є!
(2015-04-06 22:41:10) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Х–ї–µ–љ–∞, –њ—А–Њ —Д–Њ—А–Љ—Г–ї—Г —П —Б–Њ–≥–ї–∞—Б–µ–љ, –њ–Њ—Н—В–Њ–Љ—Г –Є –Њ–њ—Г–±–ї–Є–Ї–Њ–≤–∞–ї –і—А—Г–≥–Њ–є —Б–њ–Њ—Б–Њ–± - —З–µ—А–µ–Ј —В–µ–Њ—А–µ–Љ—Г —Б–Є–љ—Г—Б–Њ–≤. –Ъ 397 –Ј–∞–і–∞—З–µ —П –Њ—Б—В–∞–≤–Є–ї —Б–≤–Њ–є –Ї–Њ–Љ–Љ–µ–љ—В–∞—А–Є–є, –љ–Њ –њ–Њ–≤—В–Њ—А—О –µ–≥–Њ –Є –Ј–і–µ—Б—М. –Ы—О–±–∞—П –љ–µ—В–Њ—З–љ–Њ—Б—В—М –≤ —А–Є—Б—Г–љ–Ї–µ, –Є –Т–∞–Љ –њ—А–Є–і–µ—В—Б—П –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ —А–∞–Ј –њ—А–Є–Љ–µ–љ—П—В—М —В–µ–Њ—А–µ–Љ—Г –Я–Є—Д–∞–≥–Њ—А–∞, —З—В–Њ–±—Л –љ–∞–є—В–Є –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А. –ѓ –љ–µ —Б—З–Є—В–∞—О —Н—В–Њ—В –Љ–µ—В–Њ–і –њ—А–∞–≤–Є–ї—М–љ—Л–Љ. –І–µ—А–µ–Ј —В–µ–Њ—А–µ–Љ—Г –Ї–Њ—Б–Є–љ—Г—Б–Њ–≤ - —Н—В–Њ —Г–љ–Є–≤–µ—А—Б–∞–ї—М–љ—Л–є —Б–њ–Њ—Б–Њ–±: 1) –Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є —В–Њ—З–µ–љ, 2) –љ–µ –љ–∞–і–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ –њ—Л—В–∞—В—М—Б—П –і–Њ—Б—В—А–∞–Є–≤–∞—В—М –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А, 3) —Н—В–Њ –љ–µ —В–∞–Ї –і–Њ–ї–≥–Њ. –Ї–∞–Ї –Љ–Њ–ґ–µ—В –њ–Њ–Ї–∞–Ј–∞—В—М—Б—П, –њ—А–Њ—Б—В–Њ —П –њ–Њ–і—А–Њ–±–љ–Њ —А–∞—Б–њ–Є—Б—Л–≤–∞—О –Ї–∞–ґ–і–Њ–µ –і–µ–є—Б—В–≤–Є–µ.
(2015-04-06 21:34:32) –Х–ї–µ–љ–∞: –°–∞–Љ –њ–Њ–і—Е–Њ–і —В–Њ–ї—М–Ї–Њ —З–µ—А–µ–Ј —В–µ–Њ—А–µ–Љ—Г –Я–Є—Д–∞–≥–Њ—А–∞ —Г–љ–Є–≤–µ—А—Б–∞–ї–µ–љ. –Т 9 –Ї–ї–∞—Б—Б–µ –µ—Й—С –љ–µ –Є–Ј—Г—З–∞—О—В —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–µ —Д–Њ—А–Љ—Г–ї—Л, –Ј–∞ –Є—Б–Ї–ї—О—З–µ–љ–Є–µ–Љ –Њ—Б–љ–Њ–≤–љ–Њ–≥–Њ —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–≥–Њ —В–Њ–ґ–і–µ—Б—В–≤–∞. –Ф–∞ –љ–µ –≤–µ–Ј–і–µ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї, —В–Њ–≥–і–∞ —Б–Љ–Њ—В—А–Є –Ї–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є –Ї 397 –Ј–∞–і–∞—З–µ (–Њ–љ–∞ —А–µ—И–∞–µ—В—Б—П —В–∞–Ї–ґ–µ, –Ї–∞–Ї –Ј–∞–і–∞—З–∞ 482). –Т—А–µ–Љ—П –і–ї—П —А–µ—И–µ–љ–Є—П –њ–µ—А–≤–Њ–є —З–∞—Б—В–Є —Н–Ї–Ј–∞–Љ–µ–љ–∞ –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ, –∞ —Б —В–µ–Њ—А–µ–Љ–Њ–є –Ї–Њ—Б–Є–љ—Г—Б–Њ–≤ –љ—Г–ґ–љ–Њ –њ–Њ–≤–Њ–Ј–Є—В—М—Б—П.
(2015-04-06 20:42:05) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Х–ї–µ–љ–∞, –і–ї—П –і–∞–љ–љ–Њ–є –Ј–∞–і–∞—З–Є –њ–Њ–ї—Г—З–Є—В—Б—П —В–∞–Ї —А–µ—И–Є—В—М, –љ–Њ —А–µ—И–µ–љ–Є–µ –љ–µ —Г–љ–Є–≤–µ—А—Б–∞–ї—М–љ–Њ. –Э–µ –≤–Њ –≤—Б–µ—Е –Ј–∞–і–∞—З–∞—Е –Ј–∞–і–∞–љ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї. –≠—В—Г –Є –∞–љ–∞–ї–Њ–≥–Є—З–љ—Л–µ –Ј–∞–і–∞—З–Є –Љ–Њ–ґ–љ–Њ —А–µ—И–Є—В—М –њ–Њ —В–µ–Њ—А–µ–Љ–µ –Ї–Њ—Б–Є–љ—Г—Б–Њ–≤ (–Ї–∞–Ї –Ј–∞–і–∞—З—Г вДЦ482)
(2015-04-06 16:55:18) –Х–ї–µ–љ–∞: –Ґ—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї OBA —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є, —В.–Ї. OB=AB ( –љ–∞—Е–Њ–і–Є–Љ –Є—Е –њ–Њ —В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞ , –Ї–∞–Ї –і–Є–∞–≥–Њ–љ–∞–ї–Є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є—Е –Є–Љ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤). –Я–Њ –Ї–ї–µ—В–Ї–∞–Љ —П–≤–љ–Њ –≤–Є–і–љ–Њ —Б–µ—А–µ–і–Є–љ—Г OA (–љ–∞–Ј–Њ–≤—С–Љ –µ—С M). –Т —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ –Љ–µ–і–Є–∞–љ–∞ —П–≤–ї—П–µ—В—Б—П –≤—Л—Б–Њ—В–Њ–є, –Ј–љ–∞—З–Є—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї OMB –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є. –Я–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О —В–∞–љ–≥–µ–љ—Б–∞ tgAOB=BM/OM. –Э–∞—Е–Њ–і–Є–Љ –і–Є–∞–≥–Њ–љ–∞–ї–Є BM –Є OM –Є–Ј —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є—Е –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ –Є –Њ—В–≤–µ—В: 2. –Я—А–Є–і—С—В—Б—П –њ–Њ—А–∞–±–Њ—В–∞—В—М —Б –Ї–Њ—А–љ—П–Љ–Є, –Ј–∞—В–Њ –љ–µ –љ–∞–і–Њ –Ј–∞—Г—З–Є–≤–∞—В—М —Д–Њ—А–Љ—Г–ї—Г —В–∞–љ–≥–µ–љ—Б–∞ —А–∞–Ј–љ–Њ—Б—В–Є –і–≤—Г—Е —Г–≥–ї–Њ–≤.