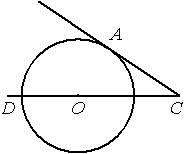
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
100°.
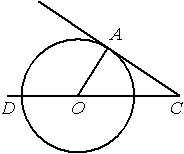Проведем отрезок ОА.
/DOA -
центральный угол для данной окружности. Он опирается на дугу AD, равную 100°. Следовательно, /DOA тоже равен 100°.
/AOC -
смежный углу DOA, поэтому /AOC=180°- /DOA=180°-100°=80°.
Треугольник ACO -
прямоугольный, т.к. радиус всегда перпендикулярен
касательной (по
свойству касательной). Т.е. /ОАС=90°. Применяя
теорему о сумме углов треугольника, можем записать:
180°=/AСO+/CAO+/AOC.
/AСO=180°-/CAO-/AOC=180°-90°-80°=10°.
Ответ: /ACO=10°.
Поделитесь решением
Присоединяйтесь к нам...
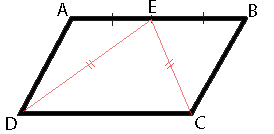В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
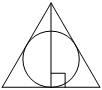Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.
Найдите площадь параллелограмма, изображённого на рисунке.
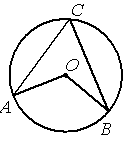Точка О – центр окружности, /ACB=62° (см. рисунок). Найдите величину угла AOB (в градусах).
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=97 и BC=BM. Найдите AH.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: