ОГЭ, Математика.
Геометрия: Задача №6AB9FA

Задача №1047 из 1087
Условие задачи:

В прямоугольном треугольнике катет и гипотенуза равны 16 и 20 соответственно. Найдите другой катет этого треугольника.

Решение задачи:

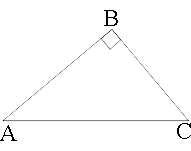Введем обозначения как показано на рисунке.
AB и BC - катеты, AC - гипотенуза.
По теореме Пифагора:
AC²=AB²+BC²
20²=AB²+16²
400=AB²+256
AB²=400-256=144
AB=√144=12
Ответ: 12

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №167EEE

В прямоугольном треугольнике один из катетов равен 7, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.

Задача №FBF9BC

Площадь прямоугольного треугольника равна 392√3. Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла.

Задача №B51630

Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=17. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.