Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
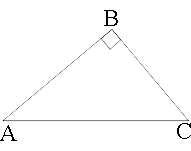Введем обозначения как показано на рисунке.
AB и BC - катеты, AC -
гипотенуза.
По
теореме Пифагора:
AC2=AB2+BC2
AC2=122+162
AC2=144+256
AC2=400
AC=√400=20
Ответ: 20
Поделитесь решением
Присоединяйтесь к нам...
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=7.
Укажите номера верных утверждений.
1) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
2) Смежные углы равны.
3) Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой.
Точка О – центр окружности, /BAC=40° (см. рисунок). Найдите величину угла BOC (в градусах).
Найдите угол ABC . Ответ дайте в градусах.
На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите её площадь.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: