
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ442 –ł–∑ 1087 |
 –í –≤—č–Ņ—É–ļ–Ľ–ĺ–ľ —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ NPQM –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć NQ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–ĺ–Ļ —É–≥–Ľ–į PNM –ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā—Ā—Ź —Ā –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć—é PM –≤ —ā–ĺ—á–ļ–Ķ S. –Ě–į–Ļ–ī–ł—ā–Ķ NS, –Ķ—Ā–Ľ–ł –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ –ĺ–ļ–ĺ–Ľ–ĺ —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į NPQM –ľ–ĺ–∂–Ĺ–ĺ –ĺ–Ņ–ł—Ā–į—ā—Ć –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć, PQ=44, SQ=22.
–í –≤—č–Ņ—É–ļ–Ľ–ĺ–ľ —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ NPQM –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć NQ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–ĺ–Ļ —É–≥–Ľ–į PNM –ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā—Ā—Ź —Ā –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć—é PM –≤ —ā–ĺ—á–ļ–Ķ S. –Ě–į–Ļ–ī–ł—ā–Ķ NS, –Ķ—Ā–Ľ–ł –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ –ĺ–ļ–ĺ–Ľ–ĺ —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į NPQM –ľ–ĺ–∂–Ĺ–ĺ –ĺ–Ņ–ł—Ā–į—ā—Ć –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć, PQ=44, SQ=22.
∠QNM - —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź
–≤–Ņ–ł—Ā–į–Ĺ–Ĺ—č–ľ –≤ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –ł –ĺ–Ņ–ł—Ä–į–Ķ—ā—Ā—Ź –Ĺ–į –ī—É–≥—É QM.
∠QPM —ā–ĺ–∂–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź
–≤–Ņ–ł—Ā–į–Ĺ–Ĺ—č–ľ –≤ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –ł –ĺ–Ņ–ł—Ä–į–Ķ—ā—Ā—Ź –Ĺ–į –ī—É–≥—É QM.
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, —ć—ā–ł —É–≥–Ľ—č —Ä–į–≤–Ĺ—č.
∠QNM=∠QPM
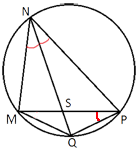 –†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł NPQ –ł SPQ.
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł NPQ –ł SPQ.
∠SQP - –ĺ–Ī—Č–ł–Ļ
∠QNP=∠SPQ
–ü–ĺ
–Ņ–Ķ—Ä–≤–ĺ–ľ—É –Ņ—Ä–ł–∑–Ĺ–į–ļ—É –Ņ–ĺ–ī–ĺ–Ī–ł—Ź —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤, –ī–į–Ĺ–Ĺ—č–Ķ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł
–Ņ–ĺ–ī–ĺ–Ī–Ĺ—č.
–Ę–ĺ–≥–ī–į, NQ/QP=QP/SQ
NQ=QP2/SQ=442/22=88
NS=NQ-SQ=88-22=66
–ě—ā–≤–Ķ—ā: NS=66
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
–£–ļ–į–∂–ł—ā–Ķ –Ĺ–ĺ–ľ–Ķ—Ä–į –≤–Ķ—Ä–Ĺ—č—Ö —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ļ.
1) –ē—Ā–Ľ–ł —ā—Ä–ł —Ā—ā–ĺ—Ä–ĺ–Ĺ—č –ĺ–ī–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł–ĺ–Ĺ–į–Ľ—Ć–Ĺ—č —ā—Ä—Ď–ľ —Ā—ā–ĺ—Ä–ĺ–Ĺ–į–ľ –ī—Ä—É–≥–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į, —ā–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł –Ņ–ĺ–ī–ĺ–Ī–Ĺ—č.
2) –°—É–ľ–ľ–į —Ā–ľ–Ķ–∂–Ĺ—č—Ö —É–≥–Ľ–ĺ–≤ —Ä–į–≤–Ĺ–į 180¬į.
3) –õ—é–Ī–į—Ź –≤—č—Ā–ĺ—ā–į —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ķ–≥–ĺ –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–ĺ–Ļ.
–ö–ĺ—Ā–ł–Ĺ—É—Ā –ĺ—Ā—ā—Ä–ĺ–≥–ĺ —É–≥–Ľ–į –ź —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ķ–Ĺ 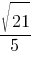 . –Ě–į–Ļ–ī–ł—ā–Ķ sinA.
. –Ě–į–Ļ–ī–ł—ā–Ķ sinA.
 –ě—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź BC –ł AD —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD —Ä–į–≤–Ĺ—č —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ 4 –ł 64, BD=16. –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł CBD –ł ADB –Ņ–ĺ–ī–ĺ–Ī–Ĺ—č.
–ě—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź BC –ł AD —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD —Ä–į–≤–Ĺ—č —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ 4 –ł 64, BD=16. –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł CBD –ł ADB –Ņ–ĺ–ī–ĺ–Ī–Ĺ—č.
 –°—ā–ĺ—Ä–ĺ–Ĺ–į —Ä–ĺ–ľ–Ī–į —Ä–į–≤–Ĺ–į 20, –į –ĺ—Ā—ā—Ä—č–Ļ —É–≥–ĺ–Ľ —Ä–į–≤–Ķ–Ĺ 60¬į. –í—č—Ā–ĺ—ā–į —Ä–ĺ–ľ–Ī–į, –ĺ–Ņ—É—Č–Ķ–Ĺ–Ĺ–į—Ź –ł–∑ –≤–Ķ—Ä—ą–ł–Ĺ—č —ā—É–Ņ–ĺ–≥–ĺ —É–≥–Ľ–į, –ī–Ķ–Ľ–ł—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—É –Ĺ–į –ī–≤–į –ĺ—ā—Ä–Ķ–∑–ļ–į. –ö–į–ļ–ĺ–≤—č –ī–Ľ–ł–Ĺ—č —ć—ā–ł—Ö –ĺ—ā—Ä–Ķ–∑–ļ–ĺ–≤?
–°—ā–ĺ—Ä–ĺ–Ĺ–į —Ä–ĺ–ľ–Ī–į —Ä–į–≤–Ĺ–į 20, –į –ĺ—Ā—ā—Ä—č–Ļ —É–≥–ĺ–Ľ —Ä–į–≤–Ķ–Ĺ 60¬į. –í—č—Ā–ĺ—ā–į —Ä–ĺ–ľ–Ī–į, –ĺ–Ņ—É—Č–Ķ–Ĺ–Ĺ–į—Ź –ł–∑ –≤–Ķ—Ä—ą–ł–Ĺ—č —ā—É–Ņ–ĺ–≥–ĺ —É–≥–Ľ–į, –ī–Ķ–Ľ–ł—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—É –Ĺ–į –ī–≤–į –ĺ—ā—Ä–Ķ–∑–ļ–į. –ö–į–ļ–ĺ–≤—č –ī–Ľ–ł–Ĺ—č —ć—ā–ł—Ö –ĺ—ā—Ä–Ķ–∑–ļ–ĺ–≤?
 –Ē–≤–Ķ –ļ–į—Ā–į—é—Č–ł–Ķ—Ā—Ź –≤–Ĺ–Ķ—ą–Ĺ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ K –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, —Ä–į–ī–ł—É—Ā—č –ļ–ĺ—ā–ĺ—Ä—č—Ö —Ä–į–≤–Ĺ—č 45 –ł 46, –≤–Ņ–ł—Ā–į–Ĺ—č –≤ —É–≥–ĺ–Ľ —Ā –≤–Ķ—Ä—ą–ł–Ĺ–ĺ–Ļ A. –ě–Ī—Č–į—Ź –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–į—Ź –ļ —ć—ā–ł–ľ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ź–ľ, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–į—Ź —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ—É K, –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—č —É–≥–Ľ–į –≤ —ā–ĺ—á–ļ–į—Ö B –ł C. –Ě–į–Ļ–ī–ł—ā–Ķ —Ä–į–ī–ł—É—Ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ĺ–ļ–ĺ–Ľ–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC.
–Ē–≤–Ķ –ļ–į—Ā–į—é—Č–ł–Ķ—Ā—Ź –≤–Ĺ–Ķ—ą–Ĺ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ K –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, —Ä–į–ī–ł—É—Ā—č –ļ–ĺ—ā–ĺ—Ä—č—Ö —Ä–į–≤–Ĺ—č 45 –ł 46, –≤–Ņ–ł—Ā–į–Ĺ—č –≤ —É–≥–ĺ–Ľ —Ā –≤–Ķ—Ä—ą–ł–Ĺ–ĺ–Ļ A. –ě–Ī—Č–į—Ź –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–į—Ź –ļ —ć—ā–ł–ľ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ź–ľ, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–į—Ź —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ—É K, –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—č —É–≥–Ľ–į –≤ —ā–ĺ—á–ļ–į—Ö B –ł C. –Ě–į–Ļ–ī–ł—ā–Ķ —Ä–į–ī–ł—É—Ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ĺ–ļ–ĺ–Ľ–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC.

–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł:
(2015-05-06 09:47:10) –°–ě–§–ė–Į –ź–Ď–Ē–£–õ–õ–ě–í–Ě–ź: –ě–≥—Ä–ĺ–ľ–Ĺ–į—Ź –Ī–Ľ–į–≥–ĺ–ī–į—Ä–Ĺ–ĺ—Ā—ā—Ć –∑–į –Ņ–ĺ–ľ–ĺ—Č—Ć –ł –ļ—Ä–ĺ–Ņ–ĺ—ā–Ľ–ł–≤—č–Ļ —ā—Ä—É–ī!!!–ī–į–Ļ –í–į–ľ –Ď–ĺ–≥ –∑–ī–ĺ—Ä–ĺ–≤—Ć—Ź –ł –Ī–Ľ–į–≥–ĺ–Ņ–ĺ–Ľ—É—á–ł—Ź!
(2014-05-29 16:56:33) –ź–Ĺ–ĺ–Ĺ–ł–ľ: –°–Ņ–į—Ā–ł–Ī–ĺ –∑–į —Ā–į–Ļ—ā, –ĺ–Ĺ –ĺ—á–Ķ–Ĺ—Ć —É–ī–ĺ–Ī–Ĺ—č–Ļ.
(2014-05-23 17:16:43) –ö—Ā–Ķ–Ĺ–ł—Ź: –Ď–ĺ–Ľ—Ć—ą–ĺ–Ķ —Ā–Ņ–į—Ā–ł–Ī–ĺ –í–į–ľ –∑–į —ā–į–ļ–ĺ–Ļ —Ā–į–Ļ—ā! –ě–≥—Ä–ĺ–ľ–Ĺ–į—Ź –Ņ–ĺ–ľ–ĺ—Č—Ć –Ņ—Ä–ł –Ņ–ĺ–ī–≥–ĺ—ā–ĺ–≤–ļ–Ķ –ļ –ď–ė–ź!
(2014-05-22 13:50:55) –ź–Ľ–Ľ–į: –í—č –ľ–ĺ–Ľ–ĺ–ī–Ķ—Ü! –ě–≥—Ä–ĺ–ľ–Ĺ–ĺ–Ķ —Ā–Ņ–į—Ā–ł–Ī–ĺ –í–į–ľ –∑–į —Ä–į–Ī–ĺ—ā—É.
(2014-05-21 14:27:40) –ź–ī–ľ–ł–Ĺ–ł—Ā—ā—Ä–į—ā–ĺ—Ä: –ē—Ā–Ľ–ł —á–Ķ—Ā—ā–Ĺ–ĺ, —ā–ĺ –ī–į, –ĺ–ī–ł–Ĺ.
(2014-05-21 11:51:05) : –≤—č –ĺ–ī–ł–Ĺ —Ä–Ķ—ą–į–Ķ—ā–Ķ –≤—Ā–Ķ –∑–į–ī–į—á–ł???
(2014-05-03 10:30:29) –ź–ī–ľ–ł–Ĺ–ł—Ā—ā—Ä–į—ā–ĺ—Ä: –õ–Ķ–Ĺ–į, —Ā–Ņ–į—Ā–ł–Ī–ĺ –∑–į —ā–Ķ–Ņ–Ľ—č–Ķ —Ā–Ľ–ĺ–≤–į! –ú—č –≤ –ļ—É—Ä—Ā–Ķ, —á—ā–ĺ –∑–į–ī–į—á –Ĺ–į —Ą–ł–Ņ–ł –ĺ—á–Ķ–Ĺ—Ć –ľ–Ĺ–ĺ–≥–ĺ. –ö –Ĺ–į–ľ –Ķ–∂–Ķ–ī–Ĺ–Ķ–≤–Ĺ–ĺ –Ņ–ĺ—Ā—ā—É–Ņ–į–Ķ—ā –ĺ—á–Ķ–Ĺ—Ć –ľ–Ĺ–ĺ–≥–ĺ –∑–į–Ņ—Ä–ĺ—Ā–ĺ–≤ –Ĺ–į –Ĺ–ĺ–≤—č–Ķ –∑–į–ī–į—á–ł, –Ĺ–į –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ľ—č –ł —Ä–Ķ–į–≥–ł—Ä—É–Ķ–ľ. –ó–į–Ņ—Ä–ĺ—Ā–ĺ–≤ —ā–į–ļ –ľ–Ĺ–ĺ–≥–ĺ, —á—ā–ĺ –ľ—č –Ĺ–Ķ —É—Ā–Ņ–Ķ–≤–į–Ķ–ľ –ł—Ö –≤—Ā–Ķ –ĺ–Ī—Ä–į–Ī–į—ā—č–≤–į—ā—Ć, —ā–į–ļ —á—ā–ĺ –Ĺ–Ķ—ā –≤—Ä–Ķ–ľ–Ķ–Ĺ–ł –Ņ—Ä–ĺ—Ä–Ķ—ą–į—ā—Ć –≤—Ā–Ķ –ĺ—Ā—ā–į–Ľ—Ć–Ĺ—č–Ķ –∑–į–ī–į—á–ł. –ē—Č–Ķ —Ä–į–∑ —Ā–Ņ–į—Ā–ł–Ī–ĺ –∑–į –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā –ļ –Ĺ–į—ą–Ķ–ľ—É —Ā–į–Ļ—ā—É –ł –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—É—é –ĺ—Ü–Ķ–Ĺ–ļ—É. –£—Ā–Ņ–Ķ—Ö–ĺ–≤ –≤ —É—á–Ķ–Ī–Ķ!!!
(2014-05-03 08:32:05) –Ľ–Ķ–Ĺ–į: —Ā–Ņ–į—Ā–ł–Ī–ĺ –≤–į–ľ –ĺ–≥—Ä–ĺ–ľ–Ĺ–Ķ–Ļ—ą–Ķ–Ķ!!!!! –≤—č –ľ–Ĺ–Ķ –ĺ—á–Ķ–Ĺ—Ć –Ņ–ĺ–ľ–ĺ–≥–į–Ķ—ā–Ķ —Ā–≤–ĺ–ł–ľ–ł —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź–ľ–ł !!!!! –∑–į–≥–Ľ—Ź–Ĺ–ł—ā–Ķ –≤ —Ą–ł–Ņ–ł. —ā–į–ľ –Ĺ–į–ľ–Ĺ–ĺ–≥–ĺ –Ī–ĺ–Ľ—Ć—ą–Ķ —É–∂–Ķ –∑–į–ī–į–Ĺ–ł–Ļ. –≤—č –Ī—č –Ĺ–Ķ –ľ–ĺ–≥–Ľ–ł –Ņ–ĺ—Ä–Ķ—ą–į—ā—Ć –ļ–į–∂–ī–ĺ–Ķ –∑–į–ī–į–Ĺ–ł–Ķ, –į –ł–Ĺ–ī–Ķ–Ĺ—ā–ł—á–Ĺ—č–Ķ –ł–ľ –Ĺ–Ķ —ā—Ä–ĺ–≥–į—ā—Ć. —á—ā–ĺ–Ī—č —Ö–ĺ—ā—Ź–Ī—č –ļ–į–ļ –Ņ—Ä–ł–ľ–Ķ—Ä–ĺ–ľ –Ī—č–Ľ–ł –Ņ–ĺ—Ä–Ķ—ą–į—ā—Ć