
 Радиус вписанной в квадрат окружности равен 7√
Радиус вписанной в квадрат окружности равен 7√
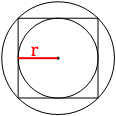 Проведем радиус
вписанной окружности, как на рисунке.
Проведем радиус
вписанной окружности, как на рисунке.
Очевидно, что r=a/2, где а - сторона
квадрата.
a=2r=2*7√
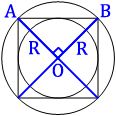 Проведем диаметры
описанной окружности, как показано на втором рисунке.
Проведем диаметры
описанной окружности, как показано на втором рисунке.
Очевидно, что
квадрат разделился на 4 равных треугольника, углы, которые опираются на центр окружности (О), равны 360°/4=90°, т.е. эти треугольники
прямоугольные.
Тогда, по теореме Пифагора:
AB2=OA2+OB2
a2=R2+R2
a2=2R2
(14√
196*2=2R2
196=R2
R=14
Ответ: 14
Поделитесь решением
Присоединяйтесь к нам...
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
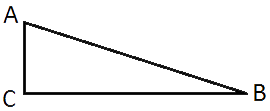 Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85.
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
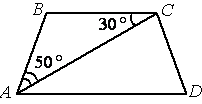 Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные
30° и 50° соответственно.
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные
30° и 50° соответственно.
 Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.

Комментарии:
(2018-02-21 23:28:59) Администратор: Анна, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2018-02-20 11:29:27) Анна: Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=24, CM=15. Найдите AO.