
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ817 –Η–Ζ 1087 |
 –ü–Μ–Ψ―â–Α–¥―¨ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α 2√
–ü–Μ–Ψ―â–Α–¥―¨ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α 2√
 –û–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ:
–û–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ:
a - –Η―¹–Κ–Ψ–Φ―΄–Ι –Κ–Α―²–Β―²
b - –≤―²–Ψ―Ä–Ψ–Ι –Κ–Α―²–Β―²
c - –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ–Α
sin60¬Α=√
sin60¬Α=a/c=√
c=2a/√
–ü–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β –ü–Η―³–Α–≥–Ψ―Ä–Α:
a2+b2=c2
a2+b2=(2a/√
a2+b2=4a2/3
3(a2+b2)=4a2
3a2+3b2=4a2
3b2=a2
b2=a2/3
b=a/√
–‰–Ζ ―É―¹–Μ–Ψ–≤–Η―è:
S―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α=ab/2=2√
a*(a/√
a2/√
a2=√
a2=4(√
a2=4
a=2
–û―²–≤–Β―²: 2
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
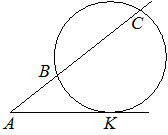 –ß–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É A, –Μ–Β–Ε–Α―â―É―é –≤–Ϋ–Β –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –¥–≤–Β –Ω―Ä―è–Φ―΄–Β. –û–¥–Ϋ–Α –Ω―Ä―è–Φ–Α―è –Κ–Α―¹–Α–Β―²―¹―è –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η
–≤ ―²–Ψ―΅–Κ–Β K. –î―Ä―É–≥–Α―è –Ω―Ä―è–Φ–Α―è –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨
–≤ ―²–Ψ―΅–Κ–Α―Ö B –Η C, –Ω―Ä–Η―΅―ë–Φ AB=2, AC=8. –ù–Α–Ι–¥–Η―²–Β AK.
–ß–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É A, –Μ–Β–Ε–Α―â―É―é –≤–Ϋ–Β –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –¥–≤–Β –Ω―Ä―è–Φ―΄–Β. –û–¥–Ϋ–Α –Ω―Ä―è–Φ–Α―è –Κ–Α―¹–Α–Β―²―¹―è –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η
–≤ ―²–Ψ―΅–Κ–Β K. –î―Ä―É–≥–Α―è –Ω―Ä―è–Φ–Α―è –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨
–≤ ―²–Ψ―΅–Κ–Α―Ö B –Η C, –Ω―Ä–Η―΅―ë–Φ AB=2, AC=8. –ù–Α–Ι–¥–Η―²–Β AK.
 –û―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è BC –Η AD ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD ―Ä–Α–≤–Ϋ―΄ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ 5 –Η 45, BD=15. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η CBD –Η BDA –Ω–Ψ–¥–Ψ–±–Ϋ―΄.
–û―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è BC –Η AD ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD ―Ä–Α–≤–Ϋ―΄ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ 5 –Η 45, BD=15. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η CBD –Η BDA –Ω–Ψ–¥–Ψ–±–Ϋ―΄.
 –ü―Ä–Ψ–Β–Κ―²–Ψ―Ä –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Ψ―¹–≤–Β―â–Α–Β―² ―ç–Κ―Ä–Α–Ϋ A –≤―΄―¹–Ψ―²–Ψ–Ι 80 ―¹–Φ, ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Ϋ―΄–Ι –Ϋ–Α ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η 250 ―¹–Φ –Ψ―² –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α. –ù–Α –Κ–Α–Κ–Ψ–Φ –Ϋ–Α–Η–Φ–Β–Ϋ―¨―à–Β–Φ ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η
(–≤ ―¹–Α–Ϋ―²–Η–Φ–Β―²―Ä–Α―Ö) –Ψ―² –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α –Ϋ―É–Ε–Ϋ–Ψ ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Η―²―¨ ―ç–Κ―Ä–Α–Ϋ B –≤―΄―¹–Ψ―²–Ψ–Ι 160 ―¹–Φ, ―΅―²–Ψ–±―΄ –Ψ–Ϋ –±―΄–Μ –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Ψ―¹–≤–Β―â―ë–Ϋ, –Β―¹–Μ–Η –Ϋ–Α―¹―²―Ä–Ψ–Ι–Κ–Η –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α –Ψ―¹―²–Α―é―²―¹―è –Ϋ–Β–Η–Ζ–Φ–Β–Ϋ–Ϋ―΄–Φ–Η?
–ü―Ä–Ψ–Β–Κ―²–Ψ―Ä –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Ψ―¹–≤–Β―â–Α–Β―² ―ç–Κ―Ä–Α–Ϋ A –≤―΄―¹–Ψ―²–Ψ–Ι 80 ―¹–Φ, ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Ϋ―΄–Ι –Ϋ–Α ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η 250 ―¹–Φ –Ψ―² –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α. –ù–Α –Κ–Α–Κ–Ψ–Φ –Ϋ–Α–Η–Φ–Β–Ϋ―¨―à–Β–Φ ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η
(–≤ ―¹–Α–Ϋ―²–Η–Φ–Β―²―Ä–Α―Ö) –Ψ―² –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α –Ϋ―É–Ε–Ϋ–Ψ ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Η―²―¨ ―ç–Κ―Ä–Α–Ϋ B –≤―΄―¹–Ψ―²–Ψ–Ι 160 ―¹–Φ, ―΅―²–Ψ–±―΄ –Ψ–Ϋ –±―΄–Μ –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Ψ―¹–≤–Β―â―ë–Ϋ, –Β―¹–Μ–Η –Ϋ–Α―¹―²―Ä–Ψ–Ι–Κ–Η –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α –Ψ―¹―²–Α―é―²―¹―è –Ϋ–Β–Η–Ζ–Φ–Β–Ϋ–Ϋ―΄–Φ–Η?
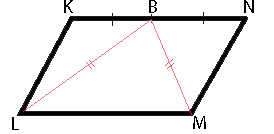 –£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β KLMN ―²–Ψ―΅–Κ–Α B βÄî ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ KN. –‰–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ BL=BM. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ –¥–Α–Ϋ–Ϋ―΄–Ι –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ βÄî –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ.
–£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β KLMN ―²–Ψ―΅–Κ–Α B βÄî ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ KN. –‰–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ BL=BM. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ –¥–Α–Ϋ–Ϋ―΄–Ι –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ βÄî –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ.
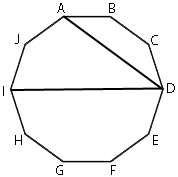 ABCDEFGHIJ βÄ™ –Ω―Ä–Α–≤–Η–Μ―¨–Ϋ―΄–Ι –¥–Β―¹―è―²–Η―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ ADI. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
ABCDEFGHIJ βÄ™ –Ω―Ä–Α–≤–Η–Μ―¨–Ϋ―΄–Ι –¥–Β―¹―è―²–Η―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ ADI. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.

–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η: