ОГЭ, Математика. Геометрия: Задача №FFBC49 | Ответ-Готов

Юмор

Автор: Таська
Так выглядит современная программа обучения.
�...читать далее

ОГЭ, Математика.
Геометрия: Задача №FFBC49

Задача №739 из 1087
Условие задачи:

Площадь прямоугольного треугольника равна 18√3/3. Один из острых углов равен 60°. Найдите длину катета, лежащего напротив этого угла.

Решение задачи:

Обозначим:
a - искомый катет
b - второй катет
c - гипотенуза
sin60°=√3/2 ( табличное значение)
sin60°=a/c=√3/2 (по определению синуса)
c=2a/√3
По теореме Пифагора:
a²+b²=c²
a²+b²=(2a/√3)²
a²+b²=4a²/3
3(a²+b²)=4a²
3a²+3b²=4a²
3b²=a²
b²=a²/3
b=a/√3
Из условия:
S_{треугольника}=ab/2=18√3/3
a*(a/√3)/2=18√3/3
a²/√3=2*18√3/3
a²=√3*36√3/3
a²=36(√3)²/3
a²=36
a=6
Ответ: 6

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №C6A628

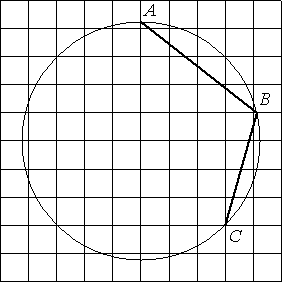Найдите угол ABC. Ответ дайте в градусах.

Задача №04BBC9

Основания BC и AD трапеции ABCD равны соответственно 4 и 64, BD=16. Докажите, что треугольники CBD и ADB подобны.

Задача №AC2DC1

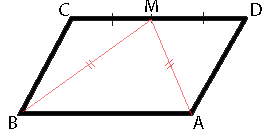В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.

Задача №116AB8

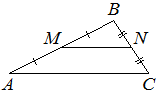Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 28, сторона BC равна 19, сторона AC равна 34. Найдите MN.

Задача №183D76

Радиус окружности с центром в точке O равен 85, длина хорды AB равна 80. Найдите расстояние от хорды AB до параллельной ей касательной k.

Комментарии:

Найти задачу

Подписаться на новости сайта

Хочу получать новые решения

email рассылки Ни какого спама

email рассылки

X Теорема Пифагора.
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

c²=a²+b²

X

Copyright otvet-gotov.ru 2014-2021. Все права защищены.