
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
Площадь прямоугольного треугольника S=AC*BC/2
Найдем AC по
теореме Пифагора:
AB2=AC2+BC2
342=AC2+302
AC2=1156-900=256
AC=16
SABC=16*30/2=8*30=240
Ответ: 240
Поделитесь решением
Присоединяйтесь к нам...
 Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.
Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.
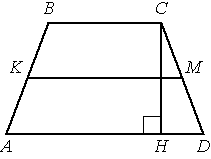 В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
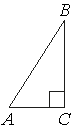 В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.
В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит меньший угол.
2) Любой квадрат можно вписать в окружность.
3) Площадь трапеции равна произведению средней линии на высоту.

Комментарии: