Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 10,5 см, а длина – 36 см. Найдите расстояние между точками A и B (в метрах).
Каждая ступенька представляет из себя
прямоугольный треугольник, следовательно расстояние между точками А и В будет равняться сумме гипотенуз ступеней.
По
теореме Пифагора:
Квадрат гипотенузы ступени равен 10,52+362=110,25+1296=1406,25
Тогда длина гипотенузы равна √
Т.к. ступеней 20 шт., то расстояние от А до В составляет 20*37,5=750 см, что равняется 7,5 м.
Ответ: 7,5
Поделитесь решением
Присоединяйтесь к нам...
Человек ростом 1,5 м стоит на расстоянии 7 м от столба, на котором висит фонарь на высоте 3,6 м. Найдите длину тени человека в метрах.
На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что
/EAB=45°. Найдите ED.
Длина хорды окружности равна 60, а расстояние от центра окружности до этой хорды равно 40. Найдите диаметр окружности.
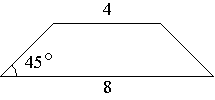В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
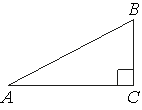В треугольнике ABC угол C равен 90°, cosB=2/5, AB=10. Найдите BC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: