
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
Площадь прямоугольного треугольника S=AC*BC/2
Найдем AC по
теореме Пифагора:
AB2=AC2+BC2
52=AC2+42
AC2=25-16=9
AC=3
SABC=3*4/2=3*2=6
Ответ: SABC=6
Поделитесь решением
Присоединяйтесь к нам...
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
 Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
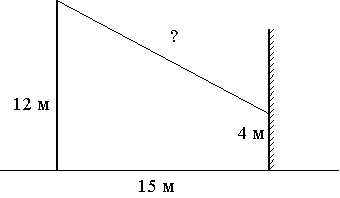 От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода. Ответ дайте в метрах.
От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода. Ответ дайте в метрах.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.
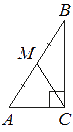 В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=60, BC=40. Найдите CM.
В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=60, BC=40. Найдите CM.

Комментарии: