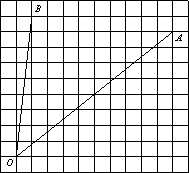
Найдите тангенс угла
AOB.
Вариант №1 (Прислал пользователь Евгений)
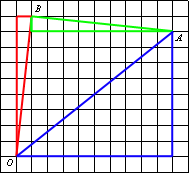Проведем отрезок AB.
Найдем каждую сторону треугольника ABO по
теореме Пифагора:
AO2=102+82
AO2=100+64=164
AO=√
AB2=92+12
AB2=81+1=82
AB=√
BO2=92+12
BO2=81+1=82
BO=√
По
теореме косинусов:
AB2=AO2+BO2-2AO*BO*cos∠AOB
(√
82=164+82-2√
-164=-2√
82=√
82=2√
41=√
cos∠AOB=41/√
По основной тригонометрической формуле:
sin2∠AOB+cos2∠AOB=1
sin2∠AOB+(1/√
sin2∠AOB+1/2=1
sin2∠AOB=1/2
sin∠AOB=1/√
tg∠AOB=sin∠AOB/cos∠AOB=(1/√
Ответ: tg∠AOB=1
Достроим чертеж до двух
прямоугольных треугольников. Найдем
тангенсы для обоих треугольников для их углов О.Поделитесь решением
Присоединяйтесь к нам...
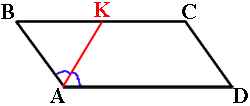Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=6, CK=10.
Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=5, AC=45.
Какие из данных утверждений верны? Запишите их номера.
1) Каждая из биссектрис равнобедренного треугольника является его высотой.
2) Диагонали прямоугольника равны.
3) У любой трапеции основания параллельны.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 45 и 46, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: