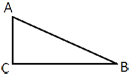
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 36 и 39.
Площадь
прямоугольного треугольника равна половине произведения катетов.
BC - катет длиной 36.
По
теореме Пифагора найдем второй катет:
AB2=AC2+BC2
392=AC2+362
1521=AC2+1296
225=AC2
AC=15
S=AC*BC/2=15*36/2=15*18=270
Ответ: S=270
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
Какие из данных утверждений верны? Запишите их номера.
1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
2) Треугольник со сторонами 1, 2, 4 не существует.
3) Сумма квадратов диагоналей прямоугольника равна сумме квадратов всех его сторон.
Проектор полностью освещает экран A высотой 190 см, расположенный
на расстоянии 210 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 380 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
Углы при одном из оснований трапеции равны 77° и 13°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 11 и 10. Найдите основания трапеции.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=3 и CH=1. Найдите cosB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-01-09 21:30:31) Администратор: Гоша, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2017-01-06 19:02:48) Гоша: Найдите площадь прямоугольного треугольника,если его катет и гипотенуза равны соответственно 18 и 30