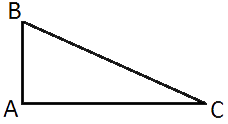
В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
SABC=AB*AC/2
Пусть угол, равный 45° будет угол В.
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
180°=90°+45°+∠C
∠C=45°
Следовательно, по
свойству равнобедренного треугольника, треугольник ABC -
равнобедренный.
Значит AB=AC.
По
теореме Пифагора:
BC2=AB2+AC2
BC2=AB2+AB2
702=2AB2
4900=2AB2
AB2=2450
SABC=AB*AC/2
SABC=AB2/2=2450/2=1225
Ответ: SABC=1225
Поделитесь решением
Присоединяйтесь к нам...
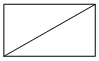В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=5, CK=14.
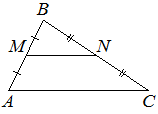Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 48, сторона BC равна 57, сторона AC равна 72. Найдите MN.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника BKP к площади треугольника AMK.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2024-02-11 01:22:37) Кристина: Найдите площадь прямоугольного треугольника, если его катет и гипоте- нуза равны соответственно 12 и 13.