
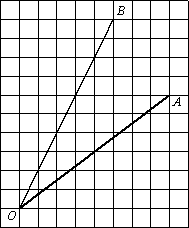
 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
Вариант №1 (Прислал пользователь Евгений)
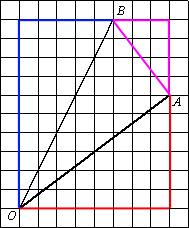 Проведем отрезок AB.
Проведем отрезок AB.
Найдем каждую сторону треугольника ABO по
теореме Пифагора:
AO2=82+62
AO2=64+36=100
AO=10
AB2=42+32
AB2=16+9=25
AB=5
BO2=102+52
BO2=100+25=125
BO=√
По
теореме косинусов:
AB2=AO2+BO2-2AO*BO*cos∠AOB
52=102+(5√
25=100+125-2*10*5√
-200=-100√
cos∠AOB=2/√
По основной тригонометрической формуле:
sin2∠AOB+cos2∠AOB=1
sin2∠AOB+4/5=1
sin2∠AOB=1/5
sin∠AOB=1/√
tg∠AOB=sin∠AOB/cos∠AOB=(1/√
Ответ: tg∠AOB=0,5
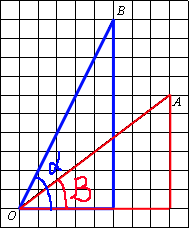 Достроим чертеж до двух
прямоугольных треугольников. Найдем
тангенсы для обоих треугольников для их углов О.
Достроим чертеж до двух
прямоугольных треугольников. Найдем
тангенсы для обоих треугольников для их углов О.Поделитесь решением
Присоединяйтесь к нам...
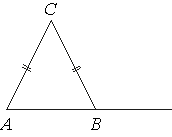 В треугольнике ABC AC=BC. Внешний угол при вершине B равен 121°. Найдите угол C. Ответ дайте в градусах.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 121°. Найдите угол C. Ответ дайте в градусах.
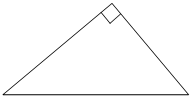 Один из острых углов прямоугольного треугольника равен 48°. Найдите его другой острый угол. Ответ дайте в градусах.
Один из острых углов прямоугольного треугольника равен 48°. Найдите его другой острый угол. Ответ дайте в градусах.
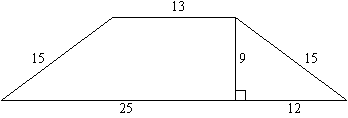 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
 Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
 В треугольнике ABC угол C равен 90°, AC=12 , tgA=2√
В треугольнике ABC угол C равен 90°, AC=12 , tgA=2√

Комментарии:
(2016-12-09 15:52:33) Администратор: Маргарита, для треугольника с красными сторонами, AO - это гипотенуза, так как лежит напротив прямого угла.
(2016-12-09 15:35:08) Маргарита: простите, забыла сообщить своё имя
(2016-12-09 15:33:20) : Поучилось какое-то недоразумение. Я написала: почему в варианте 1 AO^2 = 8^2 + 6^2 ведь AO -катет, а не гипотенуза? А в ответ мне пришло сообщение, что мой комментариий не отправлен, потому что он содержит ненормативную лексику.
(2016-12-09 00:00:00) Маргарита: Почему AO2=82+62? Ведь AO - катет, а не гипотенуза.
(2014-12-25 20:57:11) Администратор: Жанна, не во всех подобных задачах получается прямоугольный треугольник. К тому же, "дорисовать до прямоугольного треугольника" - это не точное решение, можно ошибиться. А решение не такое уж и сложное (длинное - да, но не сложное), 3 раза применяется теорема Пифагора и один раз теорема косинусов.
(2014-12-25 20:42:09) жанна: здесь легко дорисовать до прямоугольного треугольника, один катет в 2 раза больше другого
(2014-12-25 20:37:50) жанна: эти решения сложные для 9 класса
(2014-05-17 10:26:18) Администратор: Евгений, интересная мысль, мы прорешаем и выложим Ваш вариант решения. Спасибо за подсказку.
(2014-05-17 09:01:43) Евгений : можно найти косинус угла по теореме косинусов, потом найти синус и тангенс
(2014-05-12 09:19:35) Администратор: evg-bakin@yandex.ru, к сожалению, не всегда треугольник получается прямоугольным. Например, в задачах №405 и №472 треугольник очевидно не прямоугольный.
(2014-05-12 08:22:12) evg-bakin@yandex.ru: нужно построить треугольник, найти длины сторон, посмотреть будет ли этот треугольник прямоугольным. А он должен быть!
(2014-05-11 19:29:49) Администратор: Надя, да, я в курсе, но другого, строго математического решения найдено не было. Учитель математики одной школы предложил прикладывать угольник и дорисовывать до прямоугольного треугольника, но это возможно только, если разрешат пользоваться угольником на экзамене. И плюс может получиться не точно. Поэтому, думаю, что лучше запомнить эту формулу.
(2014-05-11 19:06:56) Надя: В 9 классе формула тангенса разности двух углов не изучается