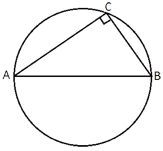
В треугольнике ABC AC=15, BC=5√
Треугольник ABC -
прямоугольный, тогда по
теореме Пифагора:
AB2=AC2+BC2
AB2=152+(5√
AB2=225+25*7
AB2=400
AB=20
Так как треугольник ABC прямоугольный, то это означает, что центр окружности находится на середине гипотенузы (по
теореме об описанной окружности).
Тогда R=AB/2=20/2=10
Ответ: R=10
Поделитесь решением
Присоединяйтесь к нам...
Периметр треугольника равен 48, одна из сторон равна 18,
а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
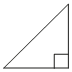В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.
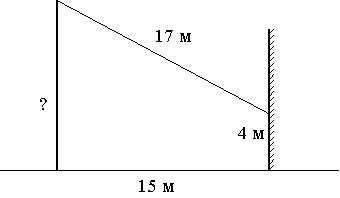От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м.
На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что
/EAB=45°. Найдите ED.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: