Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=16, BF=12.
∠GAE=∠BEA (т.к. они
накрест-лежащие)
∠GAE=∠BEA=∠BAE (т.к. AE -
биссектриса).
Получается, что треугольник ABE -
равнобедренный.
BF -
биссектриса, а по
свойству равнобедренного треугольника, она так же и
медиана и
высота.
Таким образом, получается, что треугольник ABF -
прямоугольный.
По
теореме Пифагора:
AB2=AF2+BF2
AB2=162+122
AB2=256+144=400
AB=20
Ответ: AB=20
Поделитесь решением
Присоединяйтесь к нам...
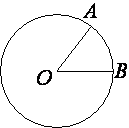На окружности с центром O отмечены точки A и B так, что
/AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги.
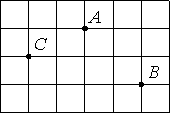На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.
Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AOD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: