
 Катет и гипотенуза прямоугольного треугольника равны 15 и 39. Найдите высоту, проведенную к гипотенузе.
Катет и гипотенуза прямоугольного треугольника равны 15 и 39. Найдите высоту, проведенную к гипотенузе.
Вариант №1
AB -
гипотенуза, BC - катет.
Найдем AC по
теореме Пифагора:
AB2=BC2+CA2
392=152+CA2
1521=225+CA2
1296=CA2
CA=36
Для треугольника ABC:
sinA=CB/AB=15/39=5/13
Для треугольника ACD:
sinA=CD/AC => CD=AC*sinA=36*5/13=180/13=13 целых и 11/13
Ответ: СD=13 целых и 11/13
Поделитесь решением
Присоединяйтесь к нам...
 Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
 Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK=18, а сторона AC в 1,2 раза больше стороны BC.
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK=18, а сторона AC в 1,2 раза больше стороны BC.
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
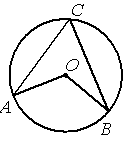 Точка О – центр окружности, /ACB=65° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=65° (см. рисунок). Найдите величину угла AOB (в градусах).
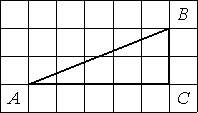 Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.

Комментарии:
(2016-04-13 14:40:14) Администратор: Даниил, Ваш вариант решения добавлен на наш сайт, спасибо Вам за решение.
(2016-04-12 23:33:56) Администратор: Даниил, обязательно рассмотрю Ваше решение.
(2016-04-10 21:48:56) Даниил: 2 вариант (мой взгляд) AB - гипотенуза, BC - катет. Найдем AC по теореме Пифагора: AB2=BC2+CA2 392=152+CA2 1521=225+CA2 1296=CA2 CA=36 S треугольника=AC*CB/2 (для прямоугольного тр) S треугольника=AB*CD/2 (т.к. CD-высота) значит AB*CD/2=AC*CB/2 39*CD=15*36 (2-ки сокращаются) CD=540/39 (15*36=540) CD=13 и 11/13