Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=20, а расстояния от центра окружности до хорд AB и CD равны соответственно 24 и 10.
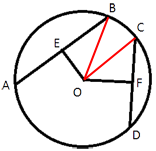Проведем отрезки OB и OC, как показано на рисунке.
Расстоянием от точки до прямой является длина перпендикуляра, проведенного к прямой. Поэтому, OE перпендикулярен AB, а OF перпендикулярен CD. Точки E и F делят свои
хорды пополам (по
свойству хорды)
Получается, что треугольники OEB и OCF -
прямоугольные, EB=AB/2 и CF=CD/2.
По
теореме Пифагора:
OB2=OE2+EB2
OB2=242+(20/2)2
OB2=576+100=676
OB=26
OB=OC=26 (т.к. OB и OC - радиусы окружности)
По
теореме Пифагора:
OC2=CF2+FO2
OC2=(CD/2)2+FO2
262=(CD/2)2+102
676=(CD/2)2+100
(CD/2)2=576
CD/2=24
CD=48
Ответ: CD=48
Поделитесь решением
Присоединяйтесь к нам...
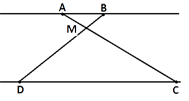Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=15, DC=30, AC=39.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=15, AC=25, NC=22.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 4. Найдите площадь трапеции.
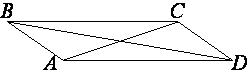В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=104°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: