Радиус вписанной в квадрат окружности равен 4√2. Найдите диагональ этого квадрата.
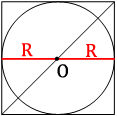Проведем радиусы окружности, как показано на рисунке.
Очевидно, что радиус вписанной окружности равен половине стороны квадрата, т.е.:
a=2R=2*4√2=8√2
По свойству квадрата, все углы прямые.
Следовательно, треугольник, образованный двумя сторонами и диагональю (обозначим ее как b) - прямоугольный.
Тогда можем применить теорему Пифагора:
b2=a2+a2
b2=2a2
b2=2(8√2)2
b2=2*64*2=256
b=√256=16
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
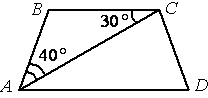Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=6, AC=10.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=123°. Найдите угол CAD. Ответ дайте в градусах.
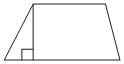Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: