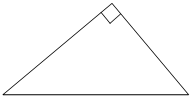
В прямоугольном треугольнике катет и гипотенуза равны 16 и 20 соответственно. Найдите другой катет этого треугольника.
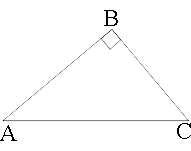Введем обозначения как показано на рисунке.
AB и BC - катеты, AC -
гипотенуза.
По
теореме Пифагора:
AC2=AB2+BC2
202=AB2+162
400=AB2+256
AB2=400-256=144
AB=√144=12
Ответ: 12
Поделитесь решением
Присоединяйтесь к нам...
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника BKP к площади треугольника AMK.
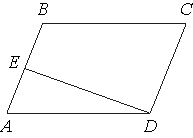Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.
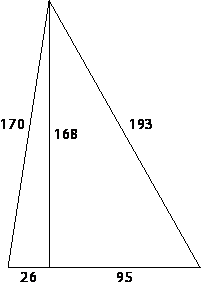Найдите площадь треугольника, изображённого на рисунке.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: