Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
Рассмотрим треугольник АОВ.
АО=ОВ, т.к. это радиусы окружности.
Следовательно, треугольник АОВ - равнобедренный.
Это значит, что ∠ОВА = ∠ОАВ = 60° (по свойству равнобедренного треугольника). Заметим, что ∠АОВ тоже равен 60° (по теореме о сумме углов треугольника). 180°-60°-60°=60°.
Следовательно, треугольник АОВ - равносторонний (по свойству равностороннего треугольника).
Получается, что ОВ=ОА=АВ=8.
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, AC=12 , tgA=2√
В треугольнике ABC известно, что AB=8, BC=10, AC=14. Найдите cos∠ABC.
Лестница соединяет точки A и B. Высота каждой ступени равна 10,5 см, а длина – 36 см. Расстояние между точками A и B составляет 15 м. Найдите высоту, на которую поднимается лестница (в метрах).
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BKC.
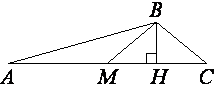В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=216, HC=54 и ∠ACB=40°. Найдите угол AMB. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
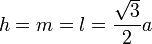
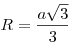
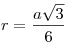
Комментарии: