Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол OVT. Ответ дайте в градусах.
SO=VO (т.к. это радиусы окружности)
SO=VO=ST=TV (по
определению ромба)
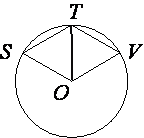Проведем отрезок OT.
OT тоже радиус окружности, следовательно OT=SO=VO=ST=TV
Следовательно, треугольники STO и TVO -
равносторонние, а все углы равностороннего треугольника равны 60° (по
свойству).
Следовательно и ∠OVT=60°
Ответ: 60
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен
90°, то такой ромб — квадрат.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
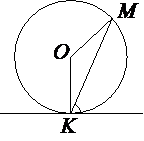Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
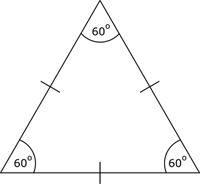
Найдите площадь треугольника, изображённого на рисунке.
Сторона квадрата равна 6√3. Найдите площадь этого квадрата.
Хочу получать новые решения
Ни какого спама
Автор: Таська
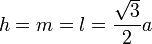
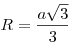
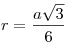
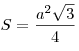
Комментарии: