
 Диагональ прямоугольника образует угол 51° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Диагональ прямоугольника образует угол 51° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
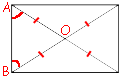 Диагонали
прямоугольника равны и точкой пересечения делятся пополам (по
свойству прямоугольника).
Диагонали
прямоугольника равны и точкой пересечения делятся пополам (по
свойству прямоугольника).
Рассмотрим треугольник ABO (см. рисунок).
AO=BO (как мы только что выяснили).
Следовательно, треугольник ABO -
равнобедренный.
По первому
свойству равнобедренного треугольника:
∠OBA=∠OAB
По
теореме о сумме углов треугольника:
180°=∠AOB+∠OBA+∠OAB
180°=∠AOB+51°+51°
180°=∠AOB+102°
∠AOB=180°-102°
∠AOB=78°
Ответ: 78
Поделитесь решением
Присоединяйтесь к нам...
 Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
 Медиана равностороннего треугольника равна 9√
Медиана равностороннего треугольника равна 9√
Укажите номера верных утверждений.
1) Существует прямоугольник, который не является параллелограммом.
2) Треугольник с углами 40° , 70°, 70° — равнобедренный.
3) Если из точки M проведены две касательные к окружности и А и В — точки касания, то отрезки MA и MB равны.
 В треугольнике ABC угол C равен 90°, BC=5, AC=3.
В треугольнике ABC угол C равен 90°, BC=5, AC=3.
Найдите tgB.
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.

Комментарии:
(2017-03-06 23:22:41) Администратор: Регина, я добавил пару строк в решение, думаю, так понятней.
(2017-03-05 14:43:00) Регина: Почему там получилось 78 если 51 +51 будет 102
(2015-05-16 07:10:01) alexey: Спасибо
(2015-05-16 07:10:01) alexey: Спасибо