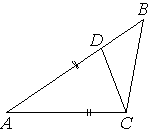
Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=19° и ∠ACB=160°. Найдите угол DCB. Ответ дайте в градусах.
Рассмотрим треугольник ACD.
По
теореме о сумме углов треугольника:
180°=∠CAB+∠ADC+∠ACD
180°=19°+∠ADC+∠ACD
∠ADC+∠ACD=161°
Так как AD=AC, то данный треугольник
равнобедренный.
Тогда, ∠ADC=∠ACD (по
свойству равнобедренного треугольника), получаем, что:
∠ADC=∠ACD=161°/2=80,5°
∠DCB=∠ACB-∠ACD=160°-80,5°=79,5°
Ответ: 79,5
Поделитесь решением
Присоединяйтесь к нам...
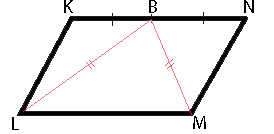В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
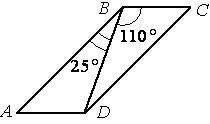Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
25° и 110°. Найдите меньший угол параллелограмма.
Какие из данных утверждений верны? Запишите их номера.
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Площадь круга меньше квадрата длины его диаметра.
3) Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб.
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=5, AC=45.
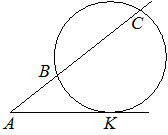Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=4, AC=64. Найдите AK.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: