
 Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
Пусть а и b -
катеты треугольника, с - гипотенуза.
Площадь
прямоугольного треугольника равна половине произведения катетов.
S=ab/2=32√
ab=64√
a=64√
По
теореме Пифагора:
c2=a2+b2
162=(64√
256b2=642*3+b4
b4-256b2+12288=0
Обозначим b2=t
t2-256t+12288=0
Решим это
квадратное уравнение:
D=(-256)2-4*12288=65536-49152=16384
√
t1=(-(-256)+128)/2=192
t2=(-(-256)-128)/2=64
Рассмотрим оба случая:
1) t=192=b2
b=√
По
определению, cosα=b/c=8√
α=30° (по
таблице)
По
теореме о сумме углов треугольника, второй острый угол равен 180°-90°-30°=60°
2) t=64=b2
b=8
По
определению, cosα=b/c=8/16=1/2
α=60° (по
таблице)
По
теореме о сумме углов треугольника, второй острый угол равен 180°-90°-60°=30°
Ответ: 30° и 60°
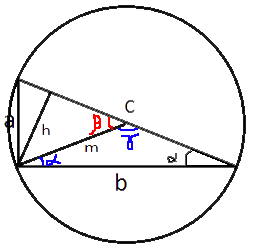 Проведем из прямого угла медиану и высоту, обозначив их m и h соответственно.
Проведем из прямого угла медиану и высоту, обозначив их m и h соответственно.Поделитесь решением
Присоединяйтесь к нам...
 Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 20, а площадь равна 50√
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 20, а площадь равна 50√
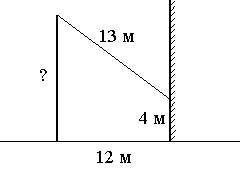 От столба к дому натянут провод длиной 13 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
От столба к дому натянут провод длиной 13 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
 Радиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции.
Радиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции.
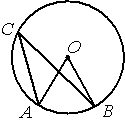 Точка О – центр окружности, /ACB=32° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=32° (см. рисунок). Найдите величину угла AOB (в градусах).
 Периметр треугольника равен 54, одна из сторон равна 15,
а радиус вписанной в него окружности равен 1. Найдите площадь этого треугольника.
Периметр треугольника равен 54, одна из сторон равна 15,
а радиус вписанной в него окружности равен 1. Найдите площадь этого треугольника.

Комментарии:
(2023-05-15 11:36:55) Алекс: Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 36,а его площадь равна 162 корня из 3
(2023-05-15 11:36:10) Алекс : Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 36,а его площадь равна 162 корня из 3