
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ717 –ł–∑ 1087 |
 –í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC AB=BC=37, AC=24. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É –ľ–Ķ–ī–ł–į–Ĺ—č BM.
–í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC AB=BC=37, AC=24. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É –ľ–Ķ–ī–ł–į–Ĺ—č BM.
–ü–ĺ —É—Ā–Ľ–ĺ–≤–ł—é –∑–į–ī–į—á–ł —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ ABC -
—Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ—č–Ļ.
BM —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ĺ–Ķ —ā–ĺ–Ľ—Ć–ļ–ĺ
–ľ–Ķ–ī–ł–į–Ĺ–ĺ–Ļ, –Ĺ–ĺ –ł
–≤—č—Ā–ĺ—ā–ĺ–Ļ (–Ņ–ĺ
—ā—Ä–Ķ—ā—Ć–Ķ–ľ—É —Ā–≤–ĺ–Ļ—Ā—ā–≤—É —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į).
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ:
1) AM=MC=AC/2=24/2=12
2) –Ę—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ ABM
–Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ļ.
–Ę–ĺ–≥–ī–į, –Ņ–ĺ
—ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –ü–ł—Ą–į–≥–ĺ—Ä–į:
AB2=BM2+AM2
372=BM2+122
1369=BM2+144
BM2=1225
BM=35
–ě—ā–≤–Ķ—ā: 35
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
 –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć –ļ–≤–į–ī—Ä–į—ā–į, –Ķ—Ā–Ľ–ł –Ķ–≥–ĺ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć —Ä–į–≤–Ĺ–į 1.
–Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć –ļ–≤–į–ī—Ä–į—ā–į, –Ķ—Ā–Ľ–ł –Ķ–≥–ĺ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć —Ä–į–≤–Ĺ–į 1.
–°–ł–Ĺ—É—Ā –ĺ—Ā—ā—Ä–ĺ–≥–ĺ —É–≥–Ľ–į A —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC —Ä–į–≤–Ķ–Ĺ 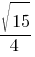 . –Ě–į–Ļ–ī–ł—ā–Ķ CosA.
. –Ě–į–Ļ–ī–ł—ā–Ķ CosA.
 –ß–Ķ–Ľ–ĺ–≤–Ķ–ļ —Ä–ĺ—Ā—ā–ĺ–ľ 1,8 –ľ —Ā—ā–ĺ–ł—ā –Ĺ–į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł 6 –ľ –ĺ—ā —Ā—ā–ĺ–Ľ–Ī–į, –Ĺ–į –ļ–ĺ—ā–ĺ—Ä–ĺ–ľ –≤–ł—Ā–ł—ā —Ą–ĺ–Ĺ–į—Ä—Ć –Ĺ–į –≤—č—Ā–ĺ—ā–Ķ 7,2 –ľ. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É —ā–Ķ–Ĺ–ł —á–Ķ–Ľ–ĺ–≤–Ķ–ļ–į –≤ –ľ–Ķ—ā—Ä–į—Ö.
–ß–Ķ–Ľ–ĺ–≤–Ķ–ļ —Ä–ĺ—Ā—ā–ĺ–ľ 1,8 –ľ —Ā—ā–ĺ–ł—ā –Ĺ–į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł 6 –ľ –ĺ—ā —Ā—ā–ĺ–Ľ–Ī–į, –Ĺ–į –ļ–ĺ—ā–ĺ—Ä–ĺ–ľ –≤–ł—Ā–ł—ā —Ą–ĺ–Ĺ–į—Ä—Ć –Ĺ–į –≤—č—Ā–ĺ—ā–Ķ 7,2 –ľ. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É —ā–Ķ–Ĺ–ł —á–Ķ–Ľ–ĺ–≤–Ķ–ļ–į –≤ –ľ–Ķ—ā—Ä–į—Ö.
 –ė–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ –ĺ–ļ–ĺ–Ľ–ĺ —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABCD –ľ–ĺ–∂–Ĺ–ĺ –ĺ–Ņ–ł—Ā–į—ā—Ć –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –ł —á—ā–ĺ –Ņ—Ä–ĺ–ī–ĺ–Ľ–∂–Ķ–Ĺ–ł—Ź —Ā—ā–ĺ—Ä–ĺ–Ĺ AB –ł CD —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –≤ —ā–ĺ—á–ļ–Ķ M. –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł MBC –ł MDA –Ņ–ĺ–ī–ĺ–Ī–Ĺ—č.
–ė–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ –ĺ–ļ–ĺ–Ľ–ĺ —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABCD –ľ–ĺ–∂–Ĺ–ĺ –ĺ–Ņ–ł—Ā–į—ā—Ć –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –ł —á—ā–ĺ –Ņ—Ä–ĺ–ī–ĺ–Ľ–∂–Ķ–Ĺ–ł—Ź —Ā—ā–ĺ—Ä–ĺ–Ĺ AB –ł CD —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –≤ —ā–ĺ—á–ļ–Ķ M. –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł MBC –ł MDA –Ņ–ĺ–ī–ĺ–Ī–Ĺ—č.
 –Ď–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į —É–≥–Ľ–į A –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į ABCD –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—É BC
–≤ —ā–ĺ—á–ļ–Ķ K. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ķ—Ä–ł–ľ–Ķ—ā—Ä –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į, –Ķ—Ā–Ľ–ł BK=7, CK=12.
–Ď–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į —É–≥–Ľ–į A –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į ABCD –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—É BC
–≤ —ā–ĺ—á–ļ–Ķ K. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ķ—Ä–ł–ľ–Ķ—ā—Ä –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į, –Ķ—Ā–Ľ–ł BK=7, CK=12.


–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł: