Площадь равнобедренного треугольника равна 1600√
Обозначим ключевые точки как показано на рисунке и проведем
высоту BD.
Высота BD так же является и
медианой, и
биссектрисой (по
третьему свойству равнобедренного треугольника).
Площадь треугольника ABC SABC=(1/2)AC*BD
Так как BD -
медиана, то AC=2AD
Тогда:
SABC=(1/2)2AD*BD=AD*BD
Так как BD еще и
биссектриса, то ∠ABD=∠ABC/2=60°
AD=AB*sin(∠ABD)=AB*sin60°
BD=AB*cos(∠ABD)=AB*cos60°
Тогда:
SABC=AB*sin60°*AB*cos60°=AB2(√
AB2/4=1600
AB2=1600*4
AB=40*2=80
Ответ: 80
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D.
Найдите CD.
Сторона ромба равна 38, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
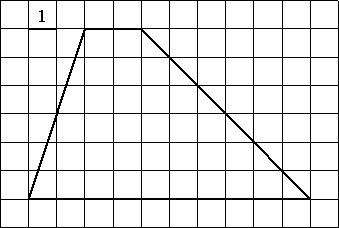Найдите площадь трапеции, изображённой на рисунке.
Какие из данных утверждений верны? Запишите их номера.
1) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
2) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти прямые параллельны.
3) У равнобедренного треугольника есть центр симметрии.
В треугольнике ABC угол C прямой, BC=8, sinA=0,4. Найдите AB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: