Площадь равнобедренного треугольника равна 196√
Обозначим ключевые точки как показано на рисунке и проведем
высоту BD.
Высота BD так же является и
медианой, и
биссектрисой (по
третьему свойству равнобедренного треугольника).
Площадь треугольника ABC SABC=(1/2)AC*BD
Так как BD -
медиана, то AC=2AD
Тогда:
SABC=(1/2)2AD*BD=AD*BD
Так как BD еще и
биссектриса, то ∠ABD=∠ABC/2=60°
AD=AB*sin(∠ABD)=AB*sin60°
BD=AB*cos(∠ABD)=AB*cos60°
Тогда:
SABC=AB*sin60°*AB*cos60°=AB2(√
AB2/4=196
AB2=784
AB=28
Ответ: 28
Поделитесь решением
Присоединяйтесь к нам...
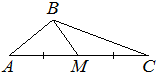В треугольнике ABC известно, что AC=54, BM — медиана, BM=43. Найдите AM.
Найдите площадь параллелограмма, изображённого на рисунке.
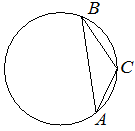В треугольнике ABC угол C равен 120°, AB=22√3. Найдите радиус окружности, описанной около этого треугольника.
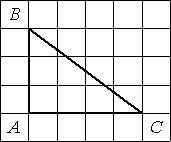Найдите тангенс угла С треугольника ABC, изображённого на рисунке.
Площадь прямоугольного треугольника равна 882√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: