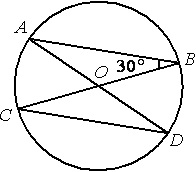В окружности с центром в точке О проведены диаметры AD и BC, угол
ABO равен 30°. Найдите величину угла ODC.
Вариант 1. Предложил пользователь Татьяна.
∠ABO=∠ABC=30°
∠ODC=∠ADC
Оба этих угла являются
вписанными и опираются на одну и ту же дугу, следовательно (по
второму свойству) они равны:
∠ABC=∠ADC=∠ODC=30°
Ответ: 30
Вариант 2.
Рассмотрим треугольник ABO. Этот треугольник
равнобедренный, т.к. ОA и ОB - радиусы, поэтому они равны.
По
свойству равнобедренного треугольника /OAB=/OBA.
Рассмотрим треугольники АОВ и COD. /DOC=/AOB, т.к. они
вертикальные. СО=DO=OB=OA, т.к. это радиусы окружности.
Следовательно, треугольники АОВ и COD равны (по
первому признаку). Поэтому /OBA=/OAB=/ODC=/OCD=30°
Ответ: /ODC=30°.
Поделитесь решением
Присоединяйтесь к нам...
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 62°, 54° и 64°.
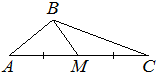В треугольнике ABC известно, что AC=38, BM — медиана, BM=17. Найдите AM.
Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Какое из следующих утверждений верно?
1) Один из двух смежных углов острый, а другой тупой.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.
В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-11-29 23:20:48) Администратор: Татьяна, да, Вы совершенно правы. Я добавлю Ваш вариант решения на сайт.
(2014-11-29 23:09:15) Татьяна: А нельзя ли эту задачу решить проще?Ведь угол ОДС и АВО - вписанные и опирающиеся на одну дугу. Следовательно, они равны, поэтому угол ОДС=30 градусов.