
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ702 –Η–Ζ 1087 |
 –ü–Μ–Ψ―â–Α–¥―¨ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α 50√
–ü–Μ–Ψ―â–Α–¥―¨ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α 50√
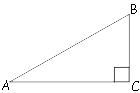 –ü–Μ–Ψ―â–Α–¥―¨
–Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α –Ω–Ψ–Μ–Ψ–≤–Η–Ϋ–Β –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η―è –Κ–Α―²–Β―²–Ψ–≤:
–ü–Μ–Ψ―â–Α–¥―¨
–Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α –Ω–Ψ–Μ–Ψ–≤–Η–Ϋ–Β –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η―è –Κ–Α―²–Β―²–Ψ–≤:
S=AC*BC/2
–ü―É―¹―²―¨ 30-–Η –≥―Ä–Α–¥―É―¹–Α–Φ ―Ä–Α–≤–Β–Ϋ ―É–≥–Ψ–Μ BAC.
–Δ–Α–Ϋ–≥–Β–Ϋ―¹ BAC:
td∠BAC=tg30¬Α=BC/AC=√
AC=BC/(√
S=(BC/(√
BC2=50√
BC=10
sin∠BAC=BC/AB (–Ω–Ψ
–Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é).
sin30¬Α=10/AB (sin30¬Α=1/2 –Ω–Ψ
―²–Α–±–Μ–Η―Ü–Β)
1/2=10/AB
AB=20
–û―²–≤–Β―²: 20
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
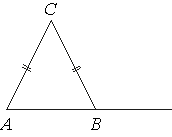 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC AC=BC. –£–Ϋ–Β―à–Ϋ–Η–Ι ―É–≥–Ψ–Μ –Ω―Ä–Η –≤–Β―Ä―à–Η–Ϋ–Β B ―Ä–Α–≤–Β–Ϋ 121¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ C. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC AC=BC. –£–Ϋ–Β―à–Ϋ–Η–Ι ―É–≥–Ψ–Μ –Ω―Ä–Η –≤–Β―Ä―à–Η–Ϋ–Β B ―Ä–Α–≤–Β–Ϋ 121¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ C. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–ù–Α –Κ–Α–Κ–Ψ–Ι ―É–≥–Ψ–Μ (–≤ –≥―Ä–Α–¥―É―¹–Α―Ö) –Ω–Ψ–≤–Ψ―Ä–Α―΅–Η–≤–Α–Β―²―¹―è –Φ–Η–Ϋ―É―²–Ϋ–Α―è ―¹―²―Ä–Β–Μ–Κ–Α, –Ω–Ψ–Κ–Α ―΅–Α―¹–Ψ–≤–Α―è –Ω―Ä–Ψ―Ö–Ψ–¥–Η―² 11¬Α?
 –£–Β―Ä―à–Η–Ϋ―΄ ―Ä–Ψ–Φ–±–Α ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ―΄ –Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ–Α―Ö –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α, –Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ ―Ä–Ψ–Φ–±–Α –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ―΄ –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―è–Φ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α. –ù–Α–Ι–¥–Η―²–Β –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η–Β –Ω–Μ–Ψ―â–Α–¥–Β–Ι ―Ä–Ψ–Φ–±–Α –Η –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α, –Β―¹–Μ–Η –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η–Β –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ–Β–Ι –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ―Ä–Α–≤–Ϋ–Ψ 31.
–£–Β―Ä―à–Η–Ϋ―΄ ―Ä–Ψ–Φ–±–Α ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ―΄ –Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ–Α―Ö –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α, –Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ ―Ä–Ψ–Φ–±–Α –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ―΄ –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―è–Φ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α. –ù–Α–Ι–¥–Η―²–Β –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η–Β –Ω–Μ–Ψ―â–Α–¥–Β–Ι ―Ä–Ψ–Φ–±–Α –Η –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α, –Β―¹–Μ–Η –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η–Β –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ–Β–Ι –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ―Ä–Α–≤–Ϋ–Ψ 31.
 –£ ―²―Ä–Α–Ω–Β―Ü–Η–Η
ABCD AB=CD, /BDA=67¬Α –Η /BDC=28¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ ABD. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–£ ―²―Ä–Α–Ω–Β―Ü–Η–Η
ABCD AB=CD, /BDA=67¬Α –Η /BDC=28¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ ABD. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC ―É–≥–Ψ–Μ C ―Ä–Α–≤–Β–Ϋ 90¬Α, tgB=3/4, BC=12. –ù–Α–Ι–¥–Η―²–Β AC.
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC ―É–≥–Ψ–Μ C ―Ä–Α–≤–Β–Ϋ 90¬Α, tgB=3/4, BC=12. –ù–Α–Ι–¥–Η―²–Β AC.
| α | sinα | cosα | tgα | ctgα |
| 0¬Α | 0 | 1 | 0 | --- |
| 30¬Α | 1/2 | √ |
√ |
√ |
| 45¬Α | √ |
√ |
1 | 1 |
| 60¬Α | √ |
1/2 | √ |
√ |
| 90¬Α | 1 | 0 | --- | 0 |
| 120¬Α | √ |
-1/2 | -√ |
0 |
| 135¬Α | √ |
-√ |
-1 | -1 |
| 150¬Α | 1/2 | -√ |
-√ |
-√ |
| 180¬Α | 0 | -1 | 0 | --- |
| 210¬Α | -1/2 | -√ |
√ |
√ |
| 225¬Α | -√ |
-√ |
1 | 1 |
| 240¬Α | -√ |
-1/2 | √ |
√ |
| 270¬Α | -1 | 0 | --- | 0 |
| 300¬Α | -√ |
1/2 | -√ |
-√ |
| 315¬Α | -√ |
√ |
-1 | -1 |
| 330¬Α | -1/2 | √ |
-√ |
-√ |
| 360¬Α | 1 | 0 | 0 | --- |
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2016-04-09 23:21:28) –ï–Μ–Β–Ϋ–Α: –Η–Ζ–≤–Η–Ϋ–Η―²–Β ―É–≤–Η–¥–Β–Μ–Α
(2016-04-09 23:21:05) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –ï–Μ–Β–Ϋ–Α, AB –Η –Β―¹―²―¨ –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ–Α, –Β–Β –¥–Μ–Η–Ϋ–Α ―Ä–Α–≤–Ϋ–Α 20.
(2016-04-09 23:20:09) –ï–Μ–Β–Ϋ–Α: –Η–Ζ–≤–Η–Ϋ–Η―²–Β,–¥–Μ–Η–Ϋ–Α –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ―΄
(2016-04-09 23:19:25) –ï–Μ–Β–Ϋ–Α: –Α –≥–¥–Β –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ–Α